

Electric Potential
Potential Differences and Electric Potential For most forces, we can construct a potential energy. As we studied Mechanics, we did this for the gravitational force and for the elastic force of a spring. These are called "conservative forces"; if we can construct a potential energy then we can use Conservation of Energy or the Work-Energy Theorem or the First Law of Thermodynamics. (Friction is a non-conservative force; it has no corresponding potential energy function). The electric force is another example of a conservative force for which we can construct a potential energy U.
It was useful to define the electric field as the force per charge,
E = F / q In a similar manner, we find it very useful to define the Potential Energy per charge, U/q; this is the electric potential V,
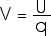
We will usually talk about the "electric potential difference between points A and B". Electric potential difference is measured in units of J/C which we call a volt
volt = V = J/C so this is also commonly referred to as the "voltage between points A and B".
As with any potential energy, all we ever see or measure or need is the change in the electric potential energy or the change in the electric potential. But it is always easier to choose some place to have zero potential energy. Then all the potential energies we talk about are the potential energy relative to that reference point. For electric situations, we choose infinity as the reference point where the electric potential energy or the electric potential is zero. Then we can talk about "the voltage at some point P". We really mean "the voltage at some point P relative to infinity" or "the voltage difference between infinity and point P" but we will usually say simply "the voltage at some point P".
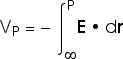
The work done or the change in potential energy
U is given by
U = q
V
We can always measure energy in units of joules (J). When we have charges q in electron charges -- like moving one electron from point A to point B -- the change in energy will probably be very small since
e = 1.6 x 10 - 19 C Therefore, it is often useful and convenient to express energy or work in units of electron-volts ( e V ),
e V = (1.6 x 10 - 19 C)(V) e V = (1.6 x 10 - 19 C)(J/C)
e V = 1.6 x 10 - 19 J
(c) Doug Davis, 2002; all rights reserved
Return to Ch25 ToC