

Gauss's Law
Example: Uniform Spherical Charge
Consider a uniform spherical distribution of charge. This must be charge held in place in an insulator. Charge on a conductor would be free to move and would end up on the surface. This charge density is uniform throughout the sphere.
Charge Q is uniformly distributed throughout a sphere of radius a. Find the electric field at a radius r.
First consider r > a; that is, find the electric field at a point outside the sphere.
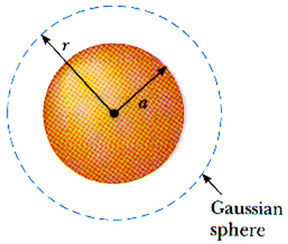
Just as before (for the point charge), we start with Gauss's Law and look at the directions involved. By symmetry (there it is, again!) we know the E-field is radially outward (assuming the charge Q is positive) so it is perpendicular to the surface. That means
E
dA = E dA

So the integral over the surface is
And Gauss's Law is that this flux through the surface is equal to the charge enclosed by the surface divided by epsilon,
Therefore,
That is, the electric field outside the sphere is exactly the same as if there were only a point charge Q.
Return to Ch24 ToC (c) Doug Davis, 2002; all rights reserved