

Gauss's Law
Example: Uniform Spherical Charge Consider a uniform spherical distribution of charge. This must be charge held in place in an insulator. Charge on a conductor would be free to move and would end up on the surface. This charge density is uniform throughout the sphere.
Charge Q is uniformly distributed throughout a sphere of radius a. Find the electric field at a radius r.
First consider r > a; that is, find the electric field at a point outside the sphere.
Just as before (for the point charge), we start with Gauss's Law
Just as for the point charge, we find
and we know
which means
E = k Q / r2 That is, the electric field outside the sphere is exactly the same as if there were only a point charge Q.
Now, move inside the sphere of uniform charge where r < a. The volumetric charge density is
The charge contained within a sphere of radius r is
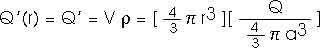

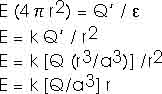
That is, the electric field inside the sphere of uniform charge is zero at the center and increases linearlywith radius r:
Of course, the two expressions for the electric field match -- have the same value -- at the surface of the sphere, for r = a.
Using Gauss's Law here made the "calculation" almost easy. A more direct application of Coulomb's Law -- with a detailed integration over the volume and a careful consideration of the vector nature of Coulomb's Law would have been far more difficult.
Return to Ch24 ToC
(c) Doug Davis, 2002; all rights reserve