Gauss's Law
Homework Solutions Questions: 3, 4, *, 13, 15
Problems: 5, 9, 12, 23, 28, *, 58, **
from the FIFTH edition of Serway & Beichner
Q3: If there are more electric field lines leaving a gaussian surface than entering, what can you conclude about the net charge enclosed by that surface?
More field lines leaving a surface than coming in means a net positive charge withing the surface. Remember, E-field lines originate on positive charges and terminate on negative charges.
Q4: A uniform electric field exists in a region of space in which there are no charges. What can you conclude about the net electric flux through a gaussian surface placed in this region of space?
With no charges present, there will be no charges within any gaussian surface so the net electric flux will (also) be zero.Q*. A point charge is placed at the center of an uncharged metallic spherical shell insulated from ground. As the point charge is moved off center, describe what happens to
(a) the total induced charge on the shell and
(b) the distribution of charge on the interior and exterior surfaces of the shell.
The total induced charge -- the sum of the charge on the interior and on the exterior -- will be zero.The distribution of the charges will change but there will be the same amount on the exterior as on the interior -- but of the opposite sign.
Q13. What would happen to the electrometer reading if the charged ball in Figure 24.20 touched the inner wall of the conductor? the outer wall?
The interior wall has no charge on it (all the charge resides on the exterior of a conductor if there is no charge inside it) so nothing will happen.The exterior wall may carry a charge which would then be transferred to the charged ball.
Q15: Two solid spheres, both of radius R, carry identical total chares, Q. One sphere is a good conductor while the other is an insulator. If the charge on the insulating sphere is uniformly distributed throughout its interior volume, how do the electric fields outside these two spheres compare? Are the fields identical inside the two spheres?
Outside the radius R, the electric fields are identical.Inside the radius R, the electric field inside the conductor is zero. Inside the radius R, the electric field inside the conductor increases linearly with radius from zero at the center.
24.5 Consider a closed triangular box resting withing a horizontal electric field of magnitude E = 7.8 x 104 N/C as shown here. Calculate the electric flux through
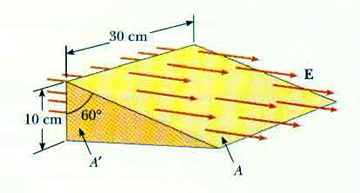
(a) the vertical surface,
(b) the slanted surface, and
(c) the entire surface of the box.
24.9 A cone of base radius R and height h is located on a horizontal table, and a horizontal uniform electric field E penetrates the cone, as shown here. Determine the electric flux entering the cone.
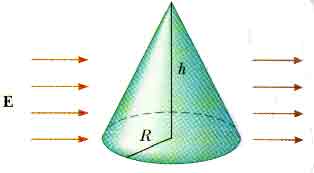
24.12 Four closed surfaces, S1 through S4, together with the charges - 2 Q, Q, and - Q are sketched here. Find the electric flux through each surface.
24.23 A charge of 170 microCoulombs, 170
C, is at the center of a cube of side 80 cm
(a) Find the total flux through each face of the cube.
(b) Find the flux through the whole surface of the cubne.
(c) Would your answers to part (a) or (b) change if the charge were not at the center?
24.28 A solid sphere of radius 40.0 cm has a total positive charge of 26.0 microCoulombs, 26
24.* Consider a solid insulating sphere of radius b with nonuniform charge density
= C r for 0 < r, b. Find the charge contained within the radius when(a) r < b and (b) when r > b.
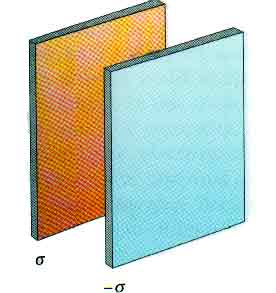
24.58 Two infinite, nonconduciting sheets of charge are parallel to each other as sketched here. The sheet on the left has a uniform surface charge density sigma
and the on on the right has a uniform charge density - sigma, -
24.** A slab of insulating material (infinite in two of its three dimensions) has a uniform positive charge density
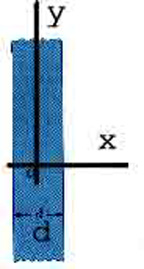
(a) Show that the electric field a distance x from its center and inside the slab is E = px/e.
(b) Suppose an electron of charge - e and mass m is placed inside the slab. If it is released from rest at a distance x from the center, show that the electron exhibits simple harmonic motion with a frequency
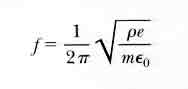
Return to Ch24 ToC (c) Doug Davis, 2002; all rights reserved
