

Gauss's Law
Gauss's Law Do you remember our introduction to Conservation of Momentum? Newton's Third Law -- "action and reaction" -- led us to the idea that the total momentum of a system remains a constant. Conservation of Momentum and Newton's Third Law are essentially restatements of the same idea. In a similiar manner we will start with Coulomb's Law and develop Gauss' Law; they are restatements of the same idea.
Consider the flux through a spherical surface due to the electric field from a point charge q at the center of the sphere:
We know the magnitude of the electric field is given by
E = k q / r2 and we know that it points radially outward. We also know that "radially outward" means it passes through the sphere perpendicular to the area. Therefore, we can write
This is just the flux through a small area. When we sum that up -- or take the integral of it -- over the whole sphere, we have
for the electric field E is constant for constant radius; E = k q/r2. The integral of dA over the sphere's surface is 4
r2. That means the total flux is
When we first looked at Coulomb's Law, F = k Qq/r2 or E = k q/r2, it was pointed out that this constant k in Coulomb's Law is sometimes written as
k = 1/4 or Coulomb's Law can be written as
E = (1/4 ) q / r2
This means the flux through our spherical surface due to a point charge q can be written as
Gauss's Law is an extension or a generalization of this. Gauss's Law is that the [net] electric flux through any closed surface is equal to the charge inside that surface divided by this constant epsilon (
).
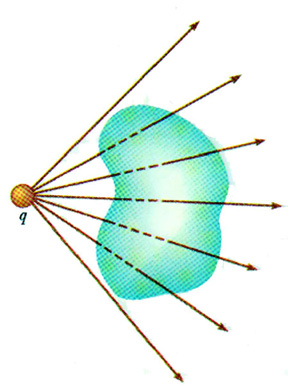
Consider several different surfaces surrounding a point charge:
Remember, we can also think of the electric flux as the number of electric field lines passing through a surface. In the diagram above, the number of lines passing through each of the different surfaces is clearly the same. That is, the flux through each of these different surfaces must be the same. The charge inside each of these surfaces is the same -- just the charge q -- so the total or net flux must also be the same.
Consider a surface with no charge inside it. The net flux is what's important. Flux is positive for electric fields E pointing out of the surface and flux is negative for electric fields E pointing into the surface.
Return to Ch24 ToC
(c) Doug Davis, 2002; all rights reserved