

Gauss's Law
Example: Cylindrical Charge Consider a line of charge with charge density of
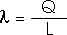
By symmetry, the electric field is everywhere radially outward, perpendicular to the line of charge.
For our "Gaussian surface" -- our surface of integration, use a cylinder with its axis of symmetry on the line of charge (as shown in the sketches here). Consider the radius r and the length L. The flux through the ends is zero since the component of the electric field E through those surfaces is zero. There is flux only through the cylindrical surface. There the electric field is perpendicular to the surface so the flux is just the electric field E multiplied by that surface;
= E ( 2
r L )
and we know, from Gauss's Law, that
= Q /

Q =
L
E ( 2
r L ) =
L /

E =
L / [
( 2
r L )]
E =
/ [
(2
r)]
E =[
/(
2
)] /r
k = 1/4


2 k = 1/ 2


E =2 k
/r
Notice that this is not an inverse-square field. The electric field from a line of charge decreases inversely as the distance from the line. It is a 1/r dependende, not a 1/r2 dependence.
Again, a direct integration would be far, far more difficult than this calculation using Gauss's Law.
Return to Ch24 ToC
(c) Doug Davis, 2002; all rights reserved