

Heat Engines, Entropy, & the Second Law
Homework Solutions
Chapter 22:
Questions 22:3, 4, 6, 16, 17
Problems 22:1, 2, 6, 7, 8, 9, 11, 28, 31, 32, 41
Be sure and do these; do not just wait and watch me do them in class!
Q22.3 Use the first law of thermodynamics to explain why the total energy of an isolated system is always constant.
The first law of thermodynamics is just a restatement of Energy Conservation. If a system is isolated no work is done on it and no heat is transferred to or from it. Energy may be transferred from one part of the system to another but the total energy remains constant.Q22.4 Is it possible to convert internal energy to mechanical energy?
The first law of thermodynamics deals with exactly that. Internal energy can be used to transfer energy in the for of heat or in the form of work.
Q22.6 In practical heat engines, which do we have more control of, the temperature of the hot reservoir or the temperature of the cold reservoir? Explain.
The cold temperature is probably going to be ambient atmospheric temperature -- perhaps the temperature of a cooling pond or a river or the ocean. There is little control over any of those. The hot temperature will be the temperature of the burning oil or coal or fissioning Uranium; that is the temperature we can control.Q22.16 Give an example of a process in nature that is nearly reversible.
Nearly eliminating friction often means the process is nearly reversible. A simple pendulum is reversible until we look at it closely enough to discover the friction from the air. Slowly compressing a balloon is nearly reversible.Q22.17 A thermodynamic process occurs in which the entropy of the system changes by - 8.0 J/K. According to the second law of thermodynamics, what can you conclude about the entropy change of the environment?
The entropy change of the environment -- the surrounding, the rest of the Universe outside our "system" -- must be + 8.0 J/K or greater so that the total energy of the Universe does not decrease.
22.1 A heat engine absorbs 360 J of thermal energy and performs 25 J of work in each cycle.
Find (a) the efficiency of the engine
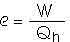
e = 25 J / 360 J
e = 0.069
e = 6.9%
and (b) the thermal energy expelled in each cycle.
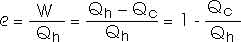
1 - [Qc/Qh] = e = 0.069
Qc/Qh = 1 - 0.069
Qc/Qh = 0.931
Qc/Qh (0.931)
Qc = (360 J) (0.931)
Qc = 335 J
22.2 A heat engine performs 200 J of work in each cycle and has an efficiency of 30%. For each cycle, how much thermal energy is
(a) absorbed and
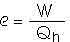
Qh = W/e
Qh = 200 J/0.30
Qh = 667 J
(b) expelled?
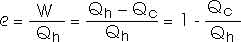
1 - [Qc/Qh] = e = 0.30
Qc/Qh = 1 - 0.30
Qc/Qh = 0.70
Qc = Qh (0.70)
Qc = (667 J) (0.70)
Qc = 467 J
22.6 A particular engine has a power output of 5.0 kW and an efficiency of 25%. If the engine expels 8 000 J of thermal energy in each cycle, find
(a) the heat absorbed in each cycle and
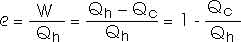
1 - [Qc/Qh] = e = 0.25
Qc/Qh = 1 - 0.25
Qc/Qh = 0.75
Qh = Qc /0.75
Qh = 8 000 J/0.75
Qh = 10 667 J
(b) the time for each cycle.
For each cycle,W = Qh - Qc
W = 10 667 J - 8 000 JW = 2 667 J = 2.667 kJ
P = W /
t
t = W / P
t = 2.667 kJ/5.0 kW
t = 0.533 s
22.7 An engine absorbs 1 600 J from a hot reservoir and expels 1 000 J to a cold reservoir in each cycle.
(a) What is the efficiency of the engine?
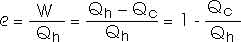
e = 1 - [ 1 000 J/1 600 J]
e = 1 - 0.625
e = 0.375
e = 37.5%
(b) What is the power output of the engine if each cycle lasts for 0.30 s?
For each cycle,W = Qh - Qc W = 1 600 J - 1 000 J
W = 600 J
Then the power is
P = W / t
P = 600 J / 0.30 s
P = 2 000 W = 2 kW
22.8 A heat engine operates between two reservoirs at 20oC and 300oC. What is the maximum efficiency possible for this engine?
From our study of Carnot engines, we know the maximum efficiency isRemember, of course, these temperatures must be measured in kelvins,
Tc = 20oC = 293 K Th = 300oC = 573 K
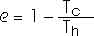
e = 1 - [ 293 K/573 K]
e = 1 - 0.511
e = 0.489
e = 48.9%
22.9 A power plant operates at a 32% efficiency during the summer when the sea water for cooling is at 20oC. The plant uses 350oC steam to drive turbines. Assuming the plant's efficiency changes in the same proportion as the ideal efficiency, what is the plant's efficiency in the winter when the sea water is at 10oC?
First, calculate the Carnot efficiencies for summer and winter,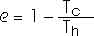
esummer = 1 - [293 K/623 K]
esummer = 1 - 0.470
esummer = 0.530
ewinter = 1 - [283 K/623 K]
ewinter = 1 - 0.454
ewinter = 0.546
Ratio = ewinter /esummer
Ratio = 0.546/0.530
Ratio = 1.03
That is, the Carnot efficiency in the winter is 1.03 times the Carnot efficiency in summer. Due to the lower cold temperature, the Carnot efficiency increases by 3%. If the real efficiency changes by 3% -- from its summer value of 32% -- then we expect a winter efficiency of
ewinter /esummer = Ratio ewinter /esummer = 1.03
ewinter = 1.03 esummer
ewinter = 1.03 (32%)
ewinter = 33%
22.11 A power plant has been proposed that would make use of thetemperature gradient in the ocean. The system is to operate between 20oC (surface water temperature) and 5oC (water temperature at a depth of about 1 km).
(a) What is the maximum efficiency of such a system?
The maximum possible efficiency is the Carnot efficiency,Tc = 5oC = 278 K Th = 20oC = 293 K
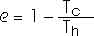
e = 1 - [ 278 K/293 K]
e = 1 - 0.949
e = 0.051
e = 5.1%
(b) If the power output of the plant is 75 MW, how much thermal energy is absorbed per hour?
First, how much work is done per hour?P = W/ t
W = P
t
W = (75 MW) (1 hr)
W = (75 x 106 W) [(J/s)/W] (1 hr) [3 600 s/hr]
W = 2.7 x 1012 J
Now, how much heat is necessary to provide that much output work?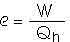
Qh = W/e
Qh = (2.7 x 1012 J) / 0.051
Qh = 5.3 x 1013 J
(c) What compensating factor made this proposal of interest despite the value of the efficiency calculated in part (a)?
There is LOTS of sea water! The temperature gradient in the ocean provides and abundant source of energy altho' the small temperature gradient means the efficiency is very low.22.14 Steam enters a turbine at 800oC and is exhausted at 120oC. What is the maximum efficiency of this turbine?
Tc = 120oC = 393 K Th = 800oC = 1073 K
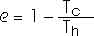
e = 1 - [ 393 K/1073 K]
e = 1 - 0.366
e = 0.634
e = 63.4%
22.28 What is the change in entropy when 1 mole of silver (108 g) is melted at 961oC?
How much heat is required to melt 108 g of silver?Q = m L Q = (0.108 kg) (8.82 x 104 J/kg)
Q = 9.53 x 103 J
S = Q/T
T = (273 + 961) K
T = 1234 K
S = (9.53 x 103 J)/(1234 K)
S = 7.72 J/K
22.31 Calculate the change in entropy of 250 g of water heated slowly from 20oC to 80oC.
(Hint: Note that dQ = m c dT).
This heat is added at different temperatures, so we must take an integral,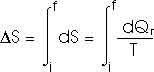
dQ = m c dT
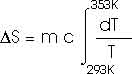
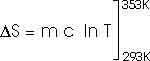

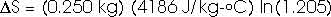
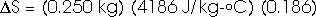
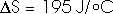
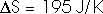
22.32 An ice tray contains 500 g of water at 0oC. Calculate the change in entropy of the water as it freezes completely and slowly at 0oC.
How much heat is required to freeze 500 g of water at 0oC?Q = m Lf
Q = (0.500 kg) (3.33 x 105 J/kg)
Q = 1.67 x 105 J
S = Q/T
S = (1.67 x 105 J)/273 K
S = 610 J/K
22.41 An 18-g ice cube at 0.0oC is heated until it vaporizes as steam.
(a) How much does the entropy increase?
How much heat is required to melt the ice cube into water at 0oC (or 273 K)?Q = m Lf Q = (0.018 kg) (3.33 x 105 J/kg)
Q = 599 J
That means the entropy added was
S = Q/T
S = (599 J)/273 K
S = 2.2 J/K
How much entropy is added as the temperature increases from 0oC to 100oC (or 373 K)? That's just like problem 22.32 that we have already solved; this, too, of course, requires an integral.
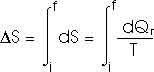
dQ = m c dT

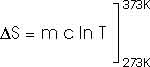
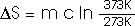
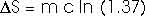
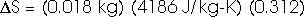
How much heat is required to vaporize the water into steam at 100oC?
Q = m Lv Q = (0.018 kg) (2.26 x 106 J/kg)
Q = 40,700 J
That means the entropy added was
S = Q/T
T = (100 + 273) K
S = (40,700 J)/373 K
S = 109 J/K
Therefore, the total entropy change is just the sum of these parts:
Stot = [2.2 + 23.5 + 109] J/K
Stot = 135 J/K
(See Table 20.2)
(b) How much energy was required to vaporize the ice cube?
We have already done (almost) all the work (ie, effort) on this, we just need to pick up the piecesQtot = Qmelt + Qraise + Qvap Qraise = m c
T
Qraise = (0.018 kg) (4186 J/kg-K) (100 K)
Qraise = 7,535 J
Qtot = Qmelt + Qraise + Qvap
Qtot = 599 J + 7,535 J + 40,700 J
Qtot = 48,834 J
(c) Doug Davis, 2002; all rights reserved
Return to ToC