

Heat Engines, Entropy, & the Second Law
Heat Engines and the Second Law The First Law of Thermodynamics is just a restatement of the Work-Energy Theorem or a restatement of the ideas of Energy Conservation. A "simple pendulum" or an "idealized pendulum" would continue to swing forever! Think of a movie or a video of a pendulum as it swings back and forth. And if we play the movie or video backward we could not distinguish it. And yet there is an arrow to time! Even pendula slow down. Drop a ball and watch it bounce. Each bounce brings the ball not quite as high as the previous bounce. A movie or a video of such a ball bouncing in the real world is different if viewed backward. Ice cubes dropped into a cup of hot tea melt while the hot tea becomes cold.
It would be consistent with the First Law of Thermodynamics if we watched a cup of room temperature tea and found ice cubes forming while the remaining tea became hot and steam arose from it. This is consistent with energy conservation. This scene would require no violation of energy conservation. But we never observe this! The Second Law of Thermodynamics will explain why (or, at least, begin to!). The Second Law of Thermodynamics deals with the "arrow of time".
Heat Engines
Consider a heat engine that takes some "working substance" -- typically a gas -- through a cyclic process. Thermal energy Qh is absorbed from a source at a hot temperature Th. Net work W is done by the heat engine on its surroundings. Thermal energy Qc is given to a source at a cold temperature Tc.
This can be represented by diagram like this --
or
We can also represent this process on a PV diagram. The net work is the area enclosed by the closed curve that represents the cyclic process.
From the First Law of Thermodynamics, we also know that the net Work W is equal to the difference between the heat absorbed Qh and the heat given up Qc. That is
W = Qh - Qc Here, we have taken both Q's to be positive.
The thermal efficiency is the ratio of the work output to the input heat Qh. That is
A typical gasoline engine might have an efficiency of about 20%. A very good diesel engine might even reach 35% to 40%.
Second Law
The Kelvin-Planck form of the Second Law of Thermodynamics may be stated as
It is impossible to construct a cyclic heat engine that produces no other effect than the absorption of heat from a reservoir and the performance of an equal amount of work.
We could sketch such an impossible heat engine as
or
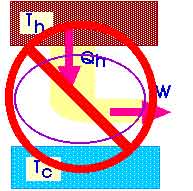
Impossible Heat Engine
This heat engine would then have a thermal efficiency of 1.00. So we could also state the Second Law as
It is impossible to construct a heat engine with an efficiency of 1.00 .
Heat Pumps and Refrigerators
A heat pump or a refrigerator is a device that absorbs heat Qc from a cold temperature and releases heat Qh at a hot temperature because work W is done to it from the outside. We could make a diagram of such a refrigerator or heat pump as
or
Just as with the (ordinary) heat engine, the First Law of Thermodynamics tells us that
W = Qh - Qc With a refrigerator or heat pump in mind, there is another form of the Second Law of Thermodynamics, called the Clausius statement which says
It is impossible to build a cyclic machine that produces no other effect than to transfer heat continuously from a cold temperature to a hot temperature.
We can make a diagram of this impossible refrigerator,
or
While these two statements of the Second Law sound like they are not connected at all, they are actually equivalent. If you could violate one form of the Second Law, you could violate the other form, too. For instance, suppose we could construct a heat engine that had 100% efficiency. It would absorb heat Qh and turn all of the energy into work W and give out no heat Qc at the cold temperature. We could then use this output work as input work for a refrigerator or heat pump.
The net result of coupling these two heat engines -- or this impossible, 100% efficient heat engine and an ordinary heat pump -- would be that heat Qc would be absorbed at the cold temperature and heat Qh would be expelled at the hot temperature.
And that result is impossible according to the "Clausius form" of the Second Law! If one form of the Second Law is violated, the other will be as well.
Return to ToC (c) Doug Davis, 2002; all rights reserved