

Kinetic Theory of Gases
Molecular Model of an Ideal Gas The "kinetic theory of gases" will allow us to make the necessary connections from the behavior of colliding particles -- energy conservation, momentum conservation, and motion in general -- to the Ideal Gas Law,
PV = n R T We will restrict this initial description to monatomic gases which we can treat as hard spheres which collide with each other and with the container walls. For these gases the only form of internal energy is the kinetic energy of translation (1/2) m v2 of the tiny spheres. For diatomic or more complicated gases -- like oxygen O2, water H2O, carbon monoxide CO2 -- we will have to also consider the energy due to rotation and vibration.
What is the connection between the microscopic motion of molecules -- which we understand from Newtonian Mechanics -- and the macroscopic characteristics we observe -- such as pressure, volume, and temperature?
Consider a single monatomic gas atom of mass m, moving with velocity v, having a component along the x-axis of vx. This gas atom is confined to a cubic container with sides of length d.
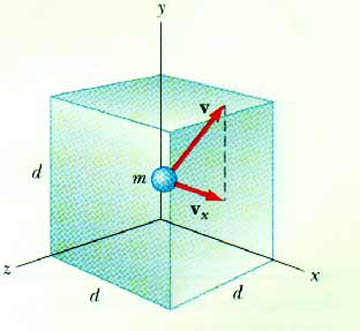
What happens when this atom strikes the container wall? In particular, consider a collision with the wall perpendicular to the x-axis. The atom undergoes an elastic collision. This means the x-component of the velocity changes sign. As it came into the wall, it was vx. After it hits the wall, it is - vx. The y- and z-components are unchanged.
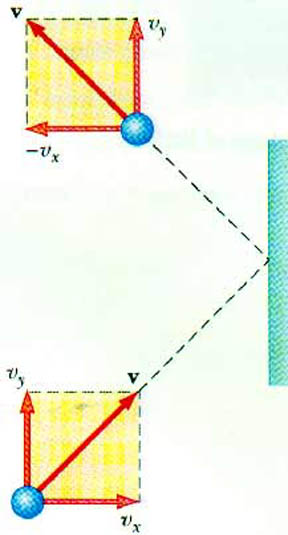
What is the change in the momentum of this atom?
px = pxf - pxi
px = - m vx - (m vx) = - 2 m vx
How are momentum and force related?
Fx = px /
t
Fx = - 2 m vx /
t
But what is
t? How long do we have to wait for this atom to strike this wall again?
t = 2 d / vx
Fx = - 2 m vx /(2 d/vx)
Fx = (m/d)(vx2)
That is the average force exerted by this single, particular atom. We might label this as F1x,
F1x = (m/d)(v1x2) Atom number 2 exerts an average force of
F2x = (m/d)(v2x2) And atom #3,
F3x = (m/d)(v3x2) So the total force, due to collisions of all the atoms, is the sum of these individual forces,
Fx = (m/d) [ v1x2 + v2x2 + v3x2 + . . . ] The average value of these vx2 terms is
That means the force on that wall, due to all the atoms, can be written as
Fx = [ N m / d ] <vx2> [[ It is easier for me to write <vx2> than it is to write
. Both notations are common.]]
You know that
v2 = vx2 + vy2 + vz2 The average value of the square of the velocity <v2> is
<v2> = <vx2> + <vy2> + <vz2> By symmetry, we also know that
<vx2> = <vy2> = <vz2> This means
<v2> = 3 <vx2> or
That's the force. Usually we are more interested in the pressure. But it's easy to convert between the two.
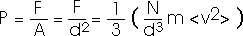
That is, the pressure is proportional to the number of atoms per volume (N/V) and to the average value of the translational kinetic energy of the atoms (1/2) m<v2>. You probably have some "physical intuition" for these ideas already. You "know" that if you blow more air into a balloon you increase its pressure. You already "know" that if you heat a gas -- that is, if you increase the energy of the atoms or molecules of the gas -- you increase its pressure.
We can turn this equation around -- we can multiply by the volume V -- to obtain
But we also know
PV = N k T where k is Boltzman's constant, k = 1.28 x 10 - 23 J/K.
That means
or
That is, the average translational kinetic energy of a molecule is (3/2) k T.
We will want to talk about each "degree of freedom" so we can also write this as
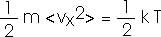
The Equipartition Theorem: the energy of a system in thermal equilibrium is equally divided among all its "degrees of freedom".
SQRT(<v2>) = vrms is called the "root mean square" speed -- the square root of the mean (average value) of the square of the speed. Such rms values will reappear as we study alternating currents in E&M.
where M = N m is the total mass of the gas. Remember k is Boltzmann's constant, k = 1.28 x 10 - 23 J/K, and R is the universal gas constant, R = 8.31 J/mol-K = 0.0821 L-atm/mol-K
Return to Ch21 ToC (c) Doug Davis, 2002; all rights reserved