

Ch20; Heat and the First Law of Thermodynamics
Applications of
The First Law of Thermodynamics
Remember an Isobaric process:Process at constant pressure:
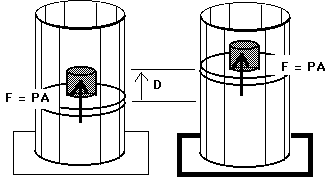
W = F D
W = ( F / A ) ( A D )
W = P ( A D )
W = P (
V)
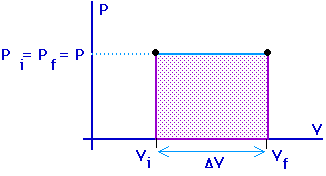
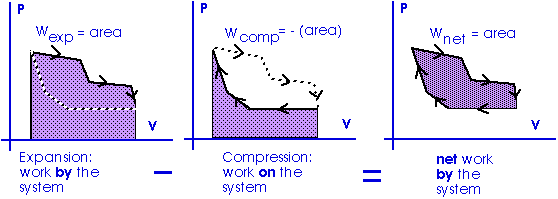
Work = area under the curve on a P-V diagram.
Work = area under the curve on a P-V diagram -- even if the process is not isobaric.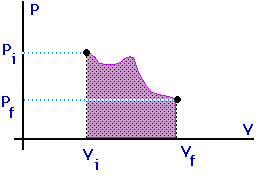
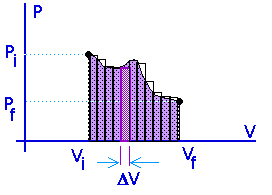
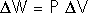
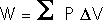
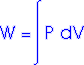
This provides a nice example of calculus.
Isometric processes:Constant volume:
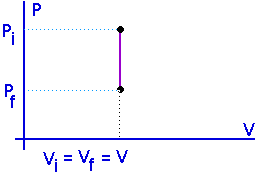
No work is done in an isometric process.
W = 0
U = Q - W
U = Q
For a constant volume process, all the heat that flows into a system goes into increasing its internal energy. This will either raise its temperature or change its state -- or both.
Isothermal process:Process at constant temperature:

We can keep the temperature constant by having the system in contact with a heat reservoir.
Adiabatic process:Process with zero heat flow:
Insulated:
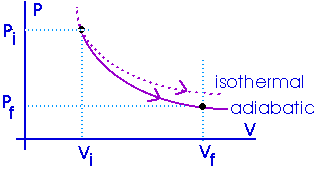
The amount of work done will be less than for an isothermal process between the same two volumes. Notice that an adiabat is steeper than an isotherm.
Q = 0
U = Q - W
U = - W
If the gas (or "the system") expands -- so it does work on its surroundings -- that energy expended as work can only come from the internal energy of the system. If the system does work on its surroundings, the internal energy must decrease. That usually means the temperature will be lowered.
Example:
W = 2.5 atm-l
Now, what is an "atmosphere-liter"? It is a pressure (atm) multiplied by a volume (liter) so it must be some sort of work or energy. Now, this is just a units conversion question,
W = 2.5 atm-l [ 0.001 m3 / 1 l ] [ 1.013 x 105 Pa / 1 atm ] W = 253 Pa-m3 [ (N/m2) / Pa ]
W = 253 N-m
W = 253 J
Return to Ch20 ToC (c) Doug Davis, 2002; all rights reserved