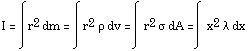
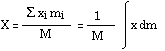
M = ![]() mi
mi
|
Possibly useful information:
| s = si + v i t + (1/2) a t2 | ac = v 2 / r | p = m v |
| v = v i + a t | W = F s cos |
PTot = p1 + p2 |
| v 2 = vi 2 + 2 a (s - si) | W = F |
PTot,i = PTot,f |
| sin |
A |
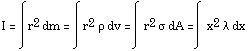
|
| cos |
A |
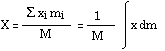
|
| tan |
dW = F x dx |
M = |
| F = m a | K = (1/2) m v2 | 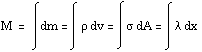
|
| F12 = - F21 | Wnet = |
|
| fsmax = µs Fn | P = |
|
| fk = µk F n | U = - W | |
| g = 9.8 m/s 2 Å 10 m/s 2 | E = K + U | |
| Ei = Ef | ||
| Fx = - [ dU / dx ] | ||
| dU = - F x dx | ||
| Fg = G Mm / r2 |
![]()
1. Momentum
Two shuffleboard disks of equal mass, one orange and the other yellow, are involved in a perfectly elastic, glancing collision. The yellow disk is initially at rest and is struck by the orange disk moving with a speed of 5.00 m/s. After the collision, the orange disk moves along a direction that makes an angle of 37.0° with its initial direction of motion, and the velocity of the yellow disk is perpendicular to that of the orange disk (after the collision -- and this will always be the case for elastic collisions between equal masses). Determine the final speed of each disk.

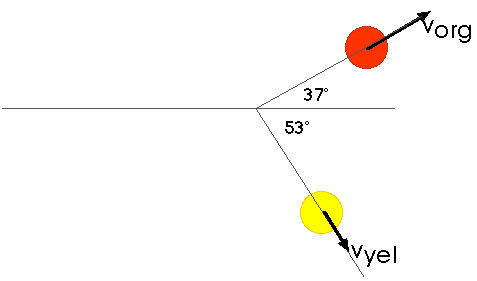
This is problem 9.45.
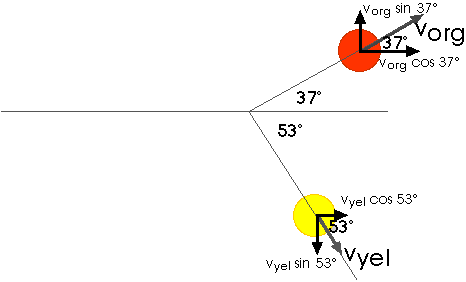
We can substitute 5.0 m/s = vo at the end.
Pfx = m vorg,x + m vyel,x
Pfx = m vorg cos 37o + m vyel cos 53o
Pfx = m vorg (0.8) + m vyel (0.6)
Pfx = m [ vorg (0.8) + vyel (0.6) ]
Pfx = m [ vorg (0.8) + vyel (0.6) ] = m vo = Pix
vorg (0.8) + vyel (0.6) = vo
Now, for the y-component,
Pfy = m vorg,y + m vyel,y
Pfy = m vorg sin 37o - m vyel sin 53o
Pfy = m vorg (0.6) - m vyel (0.8)
Pfy = m [ vorg (0.6) - vyel (0.6) ]
Pfy = m [ vorg (0.6) - vyel (0.8) ] = 0 = Piy
[ vorg (0.6) - vyel (0.8) ] = 0
Now we have two equations and two unknowns, vorg and vyel.
0.6 vorg = 0.8 vyel
vorg = 1.333 vyel
vorg (0.8) + vyel (0.6) = vo
(0.8)(1.33 vyel ) + 0.6 vyel = v o
1.667 vyel = v o
vyel = 0.6 v o
vyel = 0.6 (5.0 m/s) = 3.0 m/s
vorg = (1.333) (3.0 m/s)
vyel = 4.0 m/s
2. Rotation
A 15-kg mass and a 10-kg mass are suspended by a pulley that has a radius of 10 cm and a mass of 3.0 kg. The cord has a negligible mass and causes the pulley to rotate without slipping. The pulley rotates without friction. The masses start from rest 3.0 m apart. Treat the pulley as a uniform disk.
Idisk = (1/2) M R2
Detemine the speeds of the two masses as they pass each other.
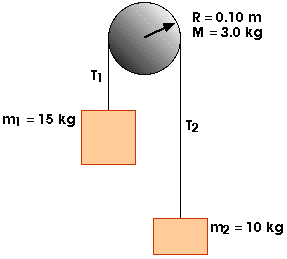
This is problem 10.32
Now, draw free-body diagrams for all three bodies,
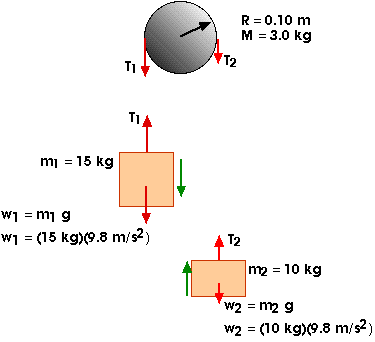
We will need the moment of inertia of the pulley,
I = (1/2) M r2 = (0.5) (3.0 kg) (0.10 m)2 = 0.015 kg m2
For mass m2, I have taken up to be positive; that means
Fnet,2 = T2 - m2 g = m2 a
For the pulley,
net =
2 -
1 = I
1 = r T1 = (0.10 m) T1
2 = r T2 = (0.10 m) T2
net =
1 -
2 = (0.10 m) T1 - (0.10 m) T2 = I
(0.10 m) [ T1 - T2 ] = I
= (0.015 kg m2)
The linear acceleration a and the angular acceleration
are related by
a = r
or
= a / r
so we may write
(0.10 m) [ T1 - T2 ] = (0.015 kg m2) a / 0.10 m
(0.10 m) [ T1 - T2 ] = (0.15 kg m) a
T1 - T2 = (1.5 kg) a
And, for mass m1, where I have taken down as positive,
FNet,1 = m1 g - T1 = m1 a
(15.0 kg) (9.8 m/s2) - T1 = (15.0 kg) a
147 N - T1 = (15.0 kg) a
Now we have three equations -- from the three free-body diagrams -- and three unknowns.
T1 = 147 N - (15.0 kg) a
T1 - T2 = (1.5 kg) a
[ 147 N - (15.0 kg) a] - T2 = (1.5 kg) a
T2 = [ 147 N - (15.0 kg) a] - (1.5 kg) a
T2 = 147 N - (16.5 kg) a
T2 - m2 g = m2 a
[147 N - (16.5 kg) a] - (10.0 kg) (9.8 m/s2) = (10.0 kg) a
147 N - 98 N = (26.5 kg) a
a = 49 N / 26.5 kg
a = 1.85 m/s2
With this acceleration of 1.85 m/s2, how fast will the blocks be moving after they have moved a distance of 1.5 m?
v2 = vo2 + 2 a (y - yo)
v2 = 02 + 2 (1.85 m/s2) (1.5 m)
v2 = 5.55 m2 / s2
v = 2.36 m/s
Alternate method, using Energy Conservation
Ei = Ef
Ei = U1i = (15 kg) (9.8 m/s2) (3.0 m) = 441 J
This takes the reference position to be the "ground", where the 10 kg mass is sitting. Since everything starts at rest, there is no kinetic energy at all.
Ef = K1 + U1 + K2 + U2 + K3
K3 = Krot = (1/2) I
2
I = = (1/2) M R2 = (0.5) (3.0 kg) (0.10 m)2 = 0.015 kg m2
K3 = Krot = (1/2) I
2 = (0.5) (0.015 kg m2)
2 = (0.0075 kg m2)
2
K2 = (1/2) m2 v2 = (0.5) (10 kg) v2 = (5 kg) v2
K1 = (1/2) m1 v2 = (0.5) (15 kg) v2 = (7.5 kg) v2
These v's are, indeed, the same. And these v's -- this velocity -- are/is related to the angular velocity
by
v = R
= (0.10 m)
= v / R = v / 0.10 m
K3 = Krot = (0.0075 kg m2) ( v / 0.10 m )2 = 0.75 kg v2
U2 = m2 g h2 = (10 kg) (9.8 m/s2) (1.5 m) = 147 J
U1 = m1 g h1 = (15 kg) (9.8 m/s2) (1.5 m) = 220.5 J
Ef = K1 + U1 + K2 + U2 + K3
Ef = 7.5 kg v2 + 220.5 J + 5 kg v2 + 147 J + 0.75 kg v2
Ef = 13.25 kg v2 + 367.5 J
Ef = Ei
13.25 kg v2 + 367.5 J = 441 J
13.25 kg v2 = 73.5 J
v2 = 5.55 m2/s2
v = 2.36 m/s
This is an example of the "joy of mathematics" -- mathematics works because it really does describe the "real world". This is the same answer we got earlier -- by a totally different method! The ideas of Physics and mathematics are useful -- and, therefore, important and worthwhile -- because they explain and predict the "real world"!
3. Angular Momentum
A merry-go-round of radius R = 2.0 m has a moment of inertia I = 250 kg m2 and is rotating at 10 rev/min. A 25-kg child jumps onto the edge of the merry-go-round.
What is the new angular speed of the merry-go-round?
This is problem 11.28
Lf = Li
L i = I i
i
Ii = 250 kg m2
i = 10 rev/min
L i = (250 kg m2) ( 10 rev/min) = 2 500 (kg m2 rev / min)
L f = I f
f
If= IMgR + Ichild
Ichild = m r2 = (25 kg) (2.0 m)2 = 100 kg m2
I f = (250 + 100) kg m2 = 350 kg m2
f = L f / I f = L i / I f = [ 2 500 kg m2 rev / min ] / [ 350 kg m2 ]
f = 7.14 rev / min
4. Calculus application
Show, by direct calculation, that the moment of inertia for a uniform rod, rotated about its Center of Mass, is (1/12) M L2.

This one is "new". This is not a duplicate of a homework problem but is quite similar to ones we did in class.
I =
r2 dm =
x2
dx =
x2
dx
I =
x2 dx =
(1/3) x3
I =
(1/3) [ ( L / 2 )3 - ( L / 2 )3 ] =
(1/3) [ L3 / 4 ]
= M / L
I = [ M / L ] (1/3) [ L3 / 4 ]
I = (1/12) M L2
(C) 1997, Doug Davis; all rights reserved