ac = v2 / r
W = F s cos
W = F
s
A
B = A B cos
A
B = Ax Bx + Ay By + Az Bz
W =
Fx dx
K = ( 1/2 ) m v2
Wnet =
K
P =
W/
t
U = - W
E = K + U
Ei = Ef
Fx = - [ dU / dx ]
U = -
Fx dx
Fg = G Mm/r2
| Return to Course Calendar | Return to Dr D's Home Page |
For every question also consider
(e) none of the above.
Be sure to put your name on the "scantron sheet" or "bubble sheet". Fill in the circles for your name. Fill in all the circles for your answers. Make any erasures complete. Put the date on the sheet (October 24, 1997)!
There are no intentionally "tricky" questions but arithmetic round-off errors can always cause problems. In my solutions I have used g = 10 m/s2. If you get an answer like 123.4 and find the only thing close is 123.5, choose that one.
This exam is multiple guess so there is no partial credit. Therefore, even more than usual, please check your work carefully and completely.
Possibly useful information:
ac = v2 / r
W = F s cos
W = F
s
A
B = A B cos
A
B = Ax Bx + Ay By + Az Bz
W =
Fx dx
K = ( 1/2 ) m v2
Wnet =
K
P =
W/
t
U = - W
E = K + U
Ei = Ef
Fx = - [ dU / dx ]
U = -
Fx dx
Fg = G Mm/r2
![]()
1. The Space Shuttle is in a low-Earth orbit where the force of gravity is nearly equal to the force of gravity at Earth's surface. Earth's radius is about 6 400 km. What is the orbital speed of the Space Shuttle?
Fg = m g = m v2 / r = Fc
v2 = g r
v2 = (10 m/s2) (6 400 000 m)
v2 = 6.4 x 107 m2/s2
v = 8 000 m/s
a) 10 m/s
b) 4 000 m/s
c) 8 000 m/s
d) 12 000 m/s
2. An automobile moves at constant speed over the crest of a hill. The driver moves in a vertical circle of radius 20.0 m. At the top of the hill, she notices that she barely remains in contact with the seat. Find the speed of the vehicle.
Since the driver "barely remains in contact with the seat", the normal force Fn, between here and the seat, is zero. She moves in a circle, so the net force on her must provide the centripetal force and the only force available is her weight, mg.
Fc = m v2 / r
Fc = m g
m v2 / r = m g
v2 / r = g
v2 = g r = ( 10 m/s2 ) ( 20 m ) = 200 m2 / s2
v = 14.14 m / s
a) 9.8 m/s
b) 14.1 m/s
c) 20 m/s
d) 200 m/s
3. A particular roller coaster has a loop-the-loop with a radius of 15 m. What is the minimum speed of the car at the top of this loop so that it does not fall off the track or that passengers do not fall out of the car?
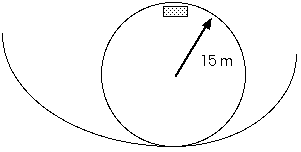
Fc = m v2 / r
Fc = Fnet = mg
That is, Fn = 0
m v2 / r = m g
v2 = g r = (10 m/s2) (15 m) = 150 m2/s2
v = 12.2 m/s
a) 10.0 m/s
b) 12.2 m/s
c) 15.5 m/s
d) 22.2 m/s
4. A particular roller coaster has a loop-the-loop with a radius of 15 m. At the top of the loop, the cars have a speed of 25 m/s. What is the normal force of the seat pushing on a 55-kg rider? This normal force will be felt as the rider's apparent weight.
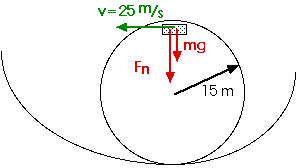
Fc = m v2 / r
Fc = Fnet = mg + Fn
m g + Fn = m v2 / r
Fn = m v2 / r - m g
Fn = m (v2 / r - g)
Fn = (55 kg) [ (25 m/s)2 / 15 m - 10 m/s2]
Fn = (55) [(625/15) - 10] N
Fn = 55 (32.67) N
Fn = 1 742 N
a) 550 N
b) 860 N
c) 1 270 N
d) 1 740 N
5. A 2.5-kg block slides down a frictionless inclined plane from rest, from an initial height of 1.0 m. How fast is it going when it reaches the bottom of the inclined plane?
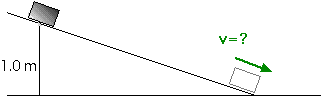
This is intended to resemble question 7.48 from the homework.
Ei = Ui + Ki = Ui = m g h = m (10 m/s2) (1 m)
Ebot = Ubot + Kbot= (1/2) m v2
(1/2) m v2 = m (10 m/s2) (1 m)
v2 = 20 m2 / s2
v = 4.47 m/s
a) 2.3 m/s
b) 4.5 m/s
c) 9.8 m/s
d) 20 m/s
6. A 3.0-kg block, initially moving with speed vo = 3 m/s, slides across a rough, horizontal plane. The coefficient of sliding friction between the block and the plane is 0.25. How far does the block slide before it comes to rest?
This is intended to resemble question 7.48 from the homework.
Wnet =
K = Kf - Ko
Kf = 0
Ko = (1/2) m v2 = 0.5 (m) (3 m/s)2
Wnet = Wf = - Ff s
Ff =
Fn
Fn = m g
Ff = (0.25) (m) (10 m/s2)
Wf = - [ (0.25) (m) (10 m/s2) ] s = - 0.5 (m) (3 m/s)2 =
K
s = (9 / 2.5) m
s = 3.6 m
a) 2.5 m
b) 3.6 m
c) 8.5 m
d) 12.6 m
7. A 1,200-kg car accelerates uniformly from rest to 12 m/s in 5.0 s. How much work done on the car in this time?
This is intended to look like question 7.57 from the homework.
W =
K
K = 0.5 m v2
W = K = (0.5) (1 200 kg) (12 m/s)2
W = 86 400 J
a) 12 000 J
b) 14 400 J
c) 86 400 J
d) 98 000 J
8. An Atwood's machine has a 3.00 kg mass and a 2.00-kg mass at ends of the string hanging over a frictionless pulley. The 2.00-kg mass is released from rest on the floor, 4.00 m below the 3.00-kg mass. What will be the speed of the masses when they pass each other?
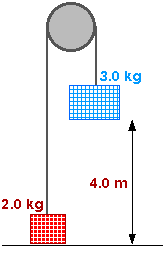
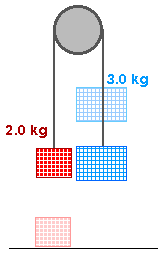
This is question 7.76 from the homework.
Wnet =
KE = KE - 0 = KE
Wnet = W2 + W3 = - (2 kg) (10 m/s2) (2 m) + (3 kg) (10 m/s2) (2 m)
Wnet = 20 J
The lower case w's in the diagram -- w2 and w3 -- are the weights;
w2 = m2 g = (2.0 kg) (10 m/s2)
w3 = m3 g = (2.0 kg) (10 m/s2)
The capital W's in the equation above -- W2 and W3 -- are the amounts of work done on the 2.0-kg mass and the 3.0-kg mass by gravity.
Only the force of gravity does work on "the system". We need not -- can not -- consider the tension in the cord for that is an "internal force" just like the forces that hold the blocks together.
The blocks have a common velocity v,
KE = 0.5 (2.0 kg) v2 + 0.5 (3.0 kg) v2 = (2.5 kg) v2
KE = (2.5 kg) v2 = 20 J = Wnet
v2 = 8 m2 / s2
v = 2.8 m / s
a) 1.4 m/s
b) 2.8 m/s
c) 3.5 m/s
d) 5.3 m/s
9. What force is associated with the potential energy, U = a x2 - b x3?
F = - dU / dx
F = - (2 a x - 3 b x2)
a) 2 a x3 - 3 b x4
b) - 2 a x + 3 b x2
c) - (1/3) a x3 + (1/4) b x4
d) (1/2) a x - (1/3) a x3
10. A potential energy function is given by U = c x + d x2. Only the force associated with this potential energy function acts on an object of mass m. The object is initially at rest at x = 5. What is its kinetic energy when it is at x = 1?
E1 = K1 + U1 = K5 + U5 = E5
U5 = 5 c + 25 d
U1 = c + d
K5 = 0
K1 = ?
K1 + (c + d) = 0 + 5c + 25 d
K1 = 4 c + 24 d
a) K = 6 c + 26 d
b) K = 5 c + 25 d
c) K = 4 c + 24 d
d) K = 2 c + 12 d
11. A 5.0-kg mass is attached to a light cord that passes over a massless, frictionless pulley. The other end of the cord is attached to a 3.5-kg mass as shown here. Use conservation of energy to determine the final speed of the 5.0-kg mass after it has fallen (starting from rest) 2.5 m.
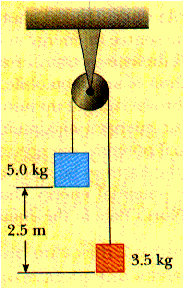
This is question 8.10 from the homework.
Ki = 0
Ui= m1 g h1 + m2 g h2
Ui = (5.0 kg) (10 m/s2) (2.5 m) + (3.5 kg) (10 m/s2) ( 0 )
Ui = 125 J
Ei = Ui + Ki = 125 J
E = constant
Ef = Ei
Ef = Kf+ Uf
Kf = Ef - Uf
Uf = (5.0 kg) (10 m/s2) ( 0 ) + (3.5 kg) (10 m/s2) (2.5 m)
Uf = 87.5 J
Kf = 125 J - 87.5 J
Kf = 37.5 J
Kf = (1/2) (5.0 kg) v2 + (1/2) (3.5 kg) v2
Kf = (1/2) (8.5 kg) v2
(1/2) (8.5 kg) v2 = 37.5 J
v2= 8.82 m2 / s2
v = 2.97 m/s
a) 1.5 m/s
b) 3.0 m/s
c) 9.0 m/s
d) 16.0 m/s
12. A 3.0-kg block starts at a height h = 60 cm = 0.60 m on a plane that has an inclination angle of 30o as shown here.
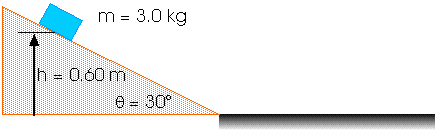
The coefficient of sliding friction between the block and the inclined plane is 0.20. What is the speed of the block at the bottom of the plane?
This is question 8.10 from the homework.
The block starts with initial total energy of
Ei = Ui + Ki
Ei= m g hi+ 0
Ei= (3 kg) (10 m/s2) (0.60 m)
Ei = 18 J
On the way down, that itinital potential energy is changed into kinetic energy and work done against friction Wf . The kinetic energy at the bottom of the incline Kbot is found by
Ei+ Wf = Ebot
Ei = Ebot - Wf = Kbot + Ubot - Wf
Kbot = Ei - Ubot + Wf
Be (very!) careful of the sign on Wf and where you place it; is this the work done by friction on the block or is the work done on the plane by the block? You can use either -- if it is clear to you which you are using and which sign that interpretation requires. To be consistent with Serway's text, we will take Wf to be the work done by friction on the block which means Wf is intrinsically negative.
W f = - F f s
From the diagram, we find
sin 30o = 0.500 = opp/hyp
s = hyp = opp/0.5 = 0.60 m/0.5
s = 1.2 m
Ff = Fn
Also, from the diagram, we find that
Fn = m g cos 30o = (3 kg) (10 m/s2) (0.866)
Fn = 26 N
Ff = (0.20) (26 N) = 5.2 N
Wf = - F f s
W f = - (5.2 N) (1.2 m)
W f = - 6.24 J
Kbot = Ei - Ubot + W f
Kbot = 18 J - 0 - 6.24 J
Kbot= 11.8 J
Kbot = 0.5 m v2 = 0.5 (3 kg) v2 = 11.8 J
v2 = 7.84 m2/s2
v = 2.8 m/s
a) 1.4 m/s
b) 2.8 m/s
c) 4.2 m/s
d) 9.8 m/s
| Return to Course Calendar | Return to Dr D's Home Page |
(C) 1997, Doug Davis; all rights reserved