Physics 1350

First Hour Exam

September 26 1997

| Return to Course Calendar | Return to Dr D's Home Page

For every question also consider

(e) none of the above.

Be sure to put your name on the "scantron sheet" or "bubble sheet". Be sure to fill in the circles for your name. Be sure to fill in all the circles for your answers. Be sure to make any erasures complete.

There are no intentionally "tricky" questions but arithmetic round-off errors can always cause problems. In my solutions I have used g = 10 m/s². If you get an answer like 123.4 and find that the only thing close is 123.5, choose that one.

Possibly useful information:

s = s_i + v_i t + (¹/₂) a t²

v = v_i + a t

v² = v_i² + 2 a (s - s_i)

sin = opp/hyp

cos = adj/hyp

tan = opp/adj

F = m a

F₁₂ = - F₂₁

f_smax = µ_s n

f_k = µ_k n

g = 9.8 m/s² = 10 m/s²

Questions 1 through 8 count 10 points each.

Questions 9 through 12 count 5 points each.

This change in points will not show up on the "tear sheet" that is returned from Academic Testing Services next week.

A hot air balloon is moving up at 5.0 m/s and is at an altitude of 10.0 m when a sandbag breaks loose and falls to the ground below

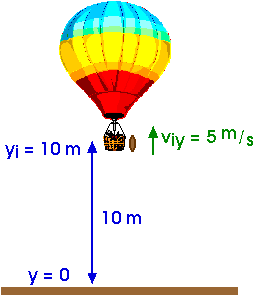
1. How long is it before the sandbag hits the ground?

y = y_i + v_i t + (1/2) a_y t²

y = y_i+ v_i t + (1/2) (- g) t²

0 = 10 m + (5 m/s) t + (1/2) (- 10 m/s²) t²

0 = 10 + 5 t + (1/2) (- 10) t²

0 = 10 + 5 t - 5 t²

5 t² - 5 t - 10 = 0

t² - t - 2 = 0

t = { - (-1) ± SQRT[ ( - 1)² - 4 (1) (-2)] }/2(1)

t = { 1 ± SQRT[ 1 + 8)] }/2(1)

t = { 1 ± SQRT[ 9] }/2

t = { 1 ± 3 }/2

t₁ = - 2/2 = - 1 = - 1 s (extaneous; throw out)

t₂ = + 4/2 = 2 = 2 s

(a) t = 1 s

(b) t = 2 s

(c) t = 4 s

(d) t = 9.8 s

2. How fast is the sandbag moving when it hits the ground?

v² = v_i² + 2 a (s - s_i)

v_y² = v_yi² + 2 a_y (y - y_i)

v_y² = (5 m/s)² + 2 ( - 10 m/s²) (0 - 10 m)

v_y² = 5² + 2 ( - 10) ( - 10 )

v_y² = 225

v_y = 15 m/s

(a) 5 m/s

(b) 10 m/s

(c) 15 m/s

(d) 20 m/s

 

A blue Jeep traveling at a constant velocity of 15 m/s (that's about 30 mi/h) passes through an intersection just as the light turns green. A red Mustang is sitting at the intersection at rest when the light turns green. Just as the Jeep passes the Mustang, the Mustang starts to accelerate at a constant acceleration of 2 m/s². The Jeep easily goes ahead of the Mustang. But the Mustang is accelerating so it eventually catches up with the Jeep and then overtakes it.

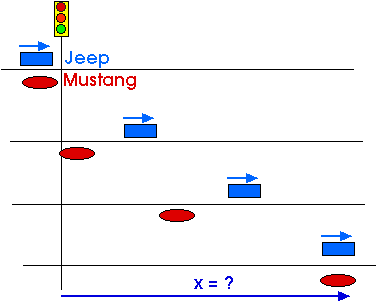
3. How far from the intersection does the Mustang catch up with the Jeep?

s = s_i + v_i t + (1/2) a t²

sm = smi + vmi t + (1/2) am t2	sj = sji + vji t + (1/2) aj t2
smi = 0; vmi = 0; am = 2 m/s2	sji = 0; vji = 15 m/s; aj = 0
sm = 0 + 0 + (1/2) (2 m/s2) t2	sj = 0 + (15 m/s) t + 0

The Mustang catches up with the Jeep when s_m = s_j

s_m = s_j

(1/2) (2 m/s²) t² = (15 m/s) t

t² = 15 t

t1 = 0; true but uninteresting

t2 = 15 = 15 sec; this is the one we want!

Now we know when the Mustang catches the Jeep; but we want to know where this happens.

s_j = (15 m/s) t

s_j = 225 m

(a) 20 m

(b) 150 m

(c) 225 m

(d) 980 m

In trying to catch the Roadrunner Wyle E Coyote speeds off a cliff with an horizontal velocity of 25 m/s. The cliff is 45 m above the canyon floor below.

4. How far from the cliff does our hapless hero hit the canyon floor?

First we find how long the coyote is in the air.

v_yi = 0

y_i = 45 m

y = y_f = 0

y = y_i + v_yi t + (1/2) a_y t²

0 = 45 m + 0 + (1/2) ( - 10 m/s²) t²

5 t² = 45

t² = 9

t = 3 = 3 s

How far horizontally does he travel in this time?

x = x_i + v_xi t + (1/2) a_x t²

x = 0 + (25 m/s) (3 s) + 0

x = 75 m

(a) 25 m

(b) 75 m

(c) 150 m

(d) 300 m

An airplane travels along the following displacement vectors:

r₁ = 300 km 30° E of N

r₂ = 400 km 60° W of N

r₃ = 100 km due West

5. Where does the airplane end up? What is its resultant displacement R?

R = r₁ + r₂ + r₃

But this means

X = x₁ + x₂ + x₃ and Y = y₁ + y₂ + y₃

Look closely at the diagram. In keeping with aviation tradition, these directions or angles are measured from north (or the positive y-axis).

x1 = r1 sin 30o	y1 = r1 cos 30o
x1 = (300 km)(0.500) = 150 km	y1 = (300 km)(0.866) = 259.8 km

Always look at your diagram and ask if it is "reasonable". Clearly, I failed to do that initially. When I incorrectly wrote down x₁ = 259.8 km and y₁ = 150 km, the diagram itself should have shown me the errors in my calculations. Take the diagrams seriously.

x2 = - (400 km) (0.866) = - 346.4 km

y2 = (400 km) (0.500) = 200 km

These values do look "reasonable" when the diagram is consulted.

x3 = - 100 km

y3 = 0

Now, we are ready for

X = x1 + x2 + x3	Y = y1 + y2 + y3
X = (150 - 346.4 - 100) km	Y = (259.8 + 200 + 0) km
X = - 296.4 km	Y = 459.8 km

Now that we have the components of R, we need to find the magnitude and direction of resultant R,

R = SQRT [ X² + Y²] = SQRT [ (- 296.4)² + (459.8)²] km = 547.1 km

= tan-1 [opp/adj] = tan-1 [X/Y] = 296.4 / 459.8 = 0.645

= 32.8°

R = 547 km, at 32.8° West of North

(a) 800 km, 53° West of North

(b) 397 km, 28° West of North

(c) 567 km, 23° East of North

(d) 247 km, 64° East of North

(e) none of the above

A 1.0 kg block slides down a plane inclined at 30° from the horizontal. The coefficient of sliding friction between the block and the plane is 0.2.

6. What is the acceleration of the block?

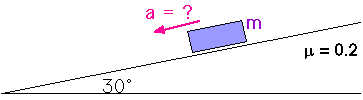
First, a free-body diagram of all the forces on the block,

F_net = w + n + f_k

Fnet,x = wx + nx + fk,x	Fnet,y = wy + ny + fk,y
Fnet,x = - w sin 30° + 0 + fk	Fnet,y = - w cos 30° + n + 0
Fnet,x = - w (0.500) + µ n	Fnet,y = - w (0.866) + n + 0 = 0 = m ay
Fnet,x = - m g (0.500) + 0.2 n	n = 0.866 w = 0.866 m g
Fnet,x = - m g (0.500) + 0.2 (0.866 m g) Fnet,x = - 0.500 m g + 0.173 m g Fnet,x = - 0.500 m g + 0.173 m g Fnet,x = - 0.327 m g = m ax ax = - 0.327 g = - 0.327 ( 10 m/s2 ) ax = - 3.27 m/s2

or, a_x = 3.27 m/s², down and to the left, along the plane

(a) a = 0.500 m/s²

(b) a = - 3.27 m/s²

(c) a = - 4.90 m/s²

(d) a = 9.6 m/s²

A 0.250 kg block is released from rest on a horizontal plane. The coefficient of friction between the block and the plane is 0.20. The block is attached, by a lightweight string, to a hanging 0.150-kg mass.

7. What is the acceleration of the block?

8. What is the tension in the string?

This should look familiar; it is the same arrangement we had in this week's lab.

As always, begin with good free-body diagrams.

First, consider the forces on M, the 0.250-kg block.

F_x = T - f_k = M a_x = M a

F_y = n - Mg = M a_y = 0

n = M g

f_k = µ n = µ M g

T - µ M g = M a

T = M a + µ M g

Now consider the forces on m, the 0.150-kg hanging mass

Down is taken as positive.

F_y = m g - T = m a_y = m a

T = m g - m a

With two expressions for the tension T,

set these two expressions equal to each other.

M a + µ M g = m g - m a

M a + m a = m g - µ M g

(M + m) a = (m - µ M) g

a = [(m - µ M) / (M + m) ] g

a = [(0.150 - {0.2}{0.25} ) / (0.250 + 0.150) ] (9.8 m/s²)

a = [(0.150 - 0.05) / 0.4 ] (9.8 m/s²)

a = [ 0.10 / 0.4 ] (9.8 m/s²)

a = (0.25) (9.8 m/s²)

a = 2.45 m/s²

Now, for the tension,

T = m g - m a = m (g - a)

T = (0.150 kg) (9.80 - 2.45) (m/s²)

T = 1.1025 N

T = 1.1 N

7. What is the acceleration of the block?

(a) a = 1.1 m/s²

(b) a = 2.45 m/s²

(c) a = 4.90 m/s²

(d) a = 9.80 m/s²

8. What is the tension in the string?

(a) T = 1.1 N

(b) T = 1.5 N

(c) T = 2.5 N

(d) T = 4.0 N

Questions 1 through 8 count 10 points each.

Questions 9 through 12 count 5 points each.

This change in points will not show up on the "tear sheet" that is returned from Academic Testing Services next week.

9. Projectile motion is a combination of

(a) horizontal motion at constant velocity and vertical motion at constant velocity

(b) horizontal motion at constant velocity and vertical motion at constant, non-zero acceleration

(c) horizontal motion at constant, non-zero acceleration and vertical motion at constant velocity

(d) horizontal motion at constant, non-zero acceleration and vertical motion at constant, non-zero acceleration

10. The force of friction depends upon the normal force. The normal force is always given by

(a) n = mg

(b) n = T

(c) n = mg sin

(d) n = mg tan

(e) none of the above -- We have no idea what angle is. The normal force can vary considerably so it is certainly not always given by any of the expressions above.

11. A block of mass m sits on a plane inclined at angle from the horizontal. The normal force of the plane on the block is

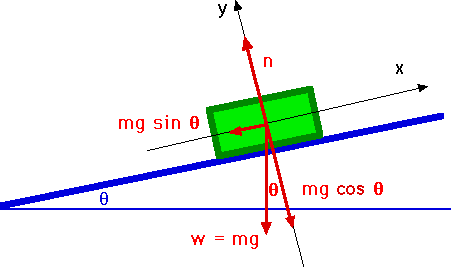
(a) n = mg

(b) n = mg cos

(c) n = mg sin

(d) n = mg tan

12. In the absence of a net force, a body in motion

(a) will gradually come to rest.

(b) will continue in motion with constant, non-zero velocity.

(c) will continue in motion with constant, non-zero acceleration

(d) will fall along a parabolic trajectory.

| Return to Course Calendar | Return to Dr D's Home Page |

(C) 1997, Doug Davis; all rights reserved