

Ch 14, The Law of Gravity
Homework: Ch14; 6, 7, 11, 21, 27, 30, 34, 57
Questions 4, 5, 8, 10, 11, 13, 14, 15, 16
(Oh, my! That's nine questions; they'd better be good!)
| Hmwk, Ch 13 | Homework Assignments | PHY 1350's Home | Hmwk, Ch 15 |
Additional problems from Serway's fourth edition
(4 ed) 14.1 If the mass of Mars is 0.107 ME and its radius is 0.53 RE, estimate the gravitational field g at the surface of Mars.
(4 ed) 14.2 Geosynchronos satellites orbit Earth with a radius of about 42 000 km. This gives them the appropriate rotational speed wrt Earth so they appear stationary in the sky. What is the force on a 1 000-kg satellite at this height?
(4 ed) 14.3 How much energy is required to move a 1 000-kg mass from Earth's surface to an altidue of h = 2 RE?
Conceptual Questions
Q14.4 Is it possible to calculate the potential energy function associated with a particle and an extended body withou knowing the geometry or mass distribution of the extended body?
No. The details of the mass distribution determine the gravitational potential function or the gravitational potential energy.
Q14.5 Does the escape speed of a rocket depend on its mass?
No. We found the escape speed with Equation 14.22, on page 441.
The mass of the rocket does not appear in that equation. A small satellite or a large space station both have the same escape speed. The escape speed depends upon the mass of the body we are escaping from (ME in this case) and the distance from the center of that body (RE in this case).
Recall that this equation has RE because it is the escape speed from the surface of Earth. If we wanted, say, the escape speed for a satellite already in a geosynchronous orbit we would need to replace RE in this equation with Rorbit, the radius of that orbit.
Q14.8 Why don't we put a geosynchronous weather satellite in orbit around the 45th parallel? Wouldn't this be more useful to the United States than such a satellite in orbit around the equator?
All satellites have planar orbits. That is the orbits of all satellites lie in a plane. That plane must pass through the center of Earth. So we can not put a satellite in an orbit that cuts through the 45th parallel.
Q14.10 Explain why no work is done on a planet as it moves in a circular orbit around the Sun, even though a gravitational force is acting on the planet. What is the net work done ona planet during each revolution as it moves around the Sun in an elliptical orbit?
In a circular orbit, the gravitational force is always perpendicular to the motion so the work done is always zero.
In an elliptical orbit, there may be a component of the gravitational force along the direction of the motion.
We already know, from Kepler's Laws of Planetary Motion, that a planet moves faster when it is closer to the Sun and that it moves slower when it is farther from the Sun. How does that fit in with work and kinetic energy?
At position A in the diagram above, as the planet is getting closer to the Sun, the force has a component in the direction of motion so positive work is done on the planet and its kinetic energy increases (or its speed increases). At position B, as it is getting farther from the Sun, the force has a component opposite to the direction of the planet so it does negative work on the planet, slowing it down (or decreasing its KE). Likewise, at position C, while it is still getting farther from the Sun, the force continues to have a component opposite to the direction of the planet so it does negative work on the planet, slowing it down (or decreasing its KE). At position D, as the planet is getting closer to the Sun, the force again has a component in the direction of motion so positive work is done on the planet causing its speed and KE to increase.
Q14.11 Explain why the force exerted on a particle by a uniform sphere must be directed toward the center of the sphere. Would this be the case if the mass distribution of the sphere were not spherically summetric?
Symmetry!
Symmetry considerations are important and (very) useful.
If the sphere is uniform, whatever "reason" you can think of that the net force might point "up" is just as good a "reason" for the net force to point "down". By symmetry, the net force must point toward the center of the sphere.
However, if the sphere is not uniform,
then there is no symmetry and you must calculate the force in its entirety -- there is no shortcut.
Q14.14 At what position in its elliptical orbit is the speed of a planet a maximum? At what position is the speed a minimum?
This is just an easy, brief application of Kepler's Laws of Planetary Motion.
A planet's speed is maximum when it is nearest the Sun.
A planet's speed is minimum when it is farthest from the Sun.
Q14.15 If a hole could be dug to the center of the Earth, do you think that the force on a mass m would still obey Equation 14.1 there? What doyou think the force n m would be at the center of Earth?
Equation 14.1, from page 424, is Newton's Law of Universal Gravitation,
Fg = G [ M1 m2 / R2 ]
and it is valid only outside the two masses M1 and m2.
At the center of Earth, symmetry demands that the force vanish. However, if we just blindly plug in R = 0 into Newton's Law of Universal Gravitation we get an undefined division by zero. So either of those results tell us that this equation does not take care of the situation of a hole drilled through our Earth.
Q14.16 In his 1798 experiment, Cavendish was said to have "weighed the Earth." Explain this statement.
Cavendish's experiment allowed him to evaluate G, the gravitational constant in Newton's Law of Universal Gravitation. Once the value of G has been determined, then the mass of the Earth can be found.
Problems from the current (5th) edition of Serway and Beichner.
14.11 A student proposes to measure the gravitational constant G by suspending two spherical masses from the ceiling of a tall cathedral and measuring the deflection from the vertical. If two 100-kg masses are suspended at the end of 45-m-long cables, and the cables are attached to the ceiling 1.000 m apart, what is the separation of the masses?
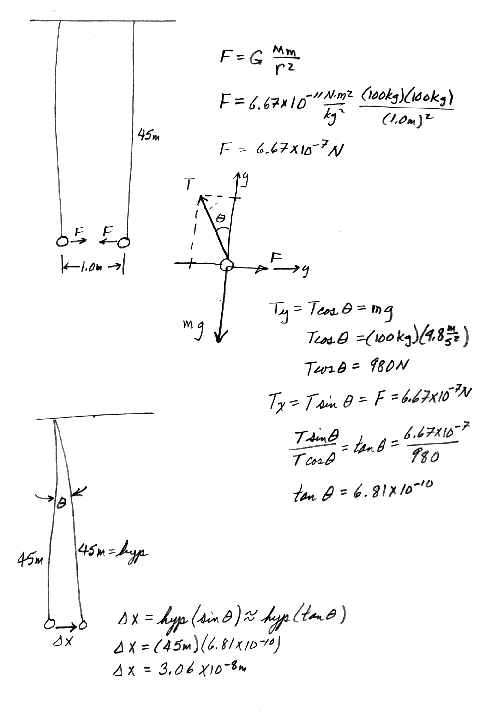
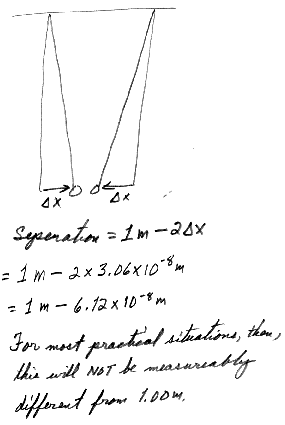
14.6 The free-fall acceleration on the surface of the Moon is about one-sixth
that on the surface of Earth. If the radius of the Moon is about 0.25 RE,
find the ratio of their densities, ![]() Moon/
Moon/ ![]() Earth.
Earth.
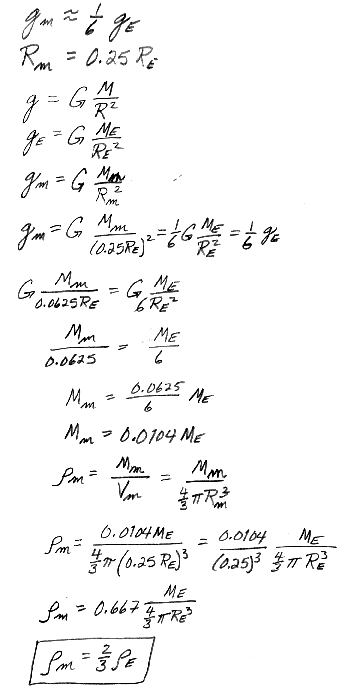
14.7 During a solar eclipse, the Moon, Earth, and Sun all lie on the same line, with the Moon between Earth and the Sun.
(a) What force is exerted on the Moon by the Sun?
(b) What force is exerted on the Moon by Earth?
(c) What force is exerted on Earth by the Sun?
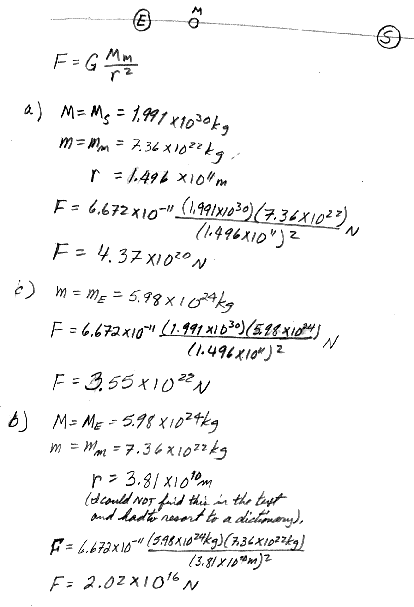
14.21 A synchronous satellite, which always remains above the same point on a planet's equator, is put in orbit around Jupiter to study the famous red spot. Jupiter rotates once every 9.9 h. Use the data of Table 14.2 to find the altitude of the satellite.
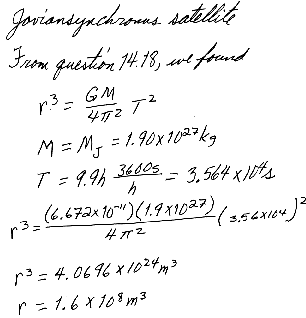
14.27 A satellite of Earth has a mass of 100 kg and is at an altitude of 2.0 x 106 m.
(a) What is the potential energy of the satellite-Earth system?
(b) What is the magnitude of the gravitational force exerted by Earth on the satellite?
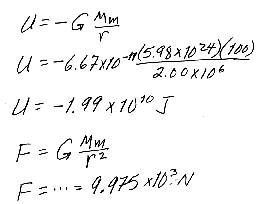
14.38 A 1 000-kg satellite orbits earth at an altitude of 100 km. It is desired to increase the altitude of the orbit to 200 km. How much energy must be added to the system to effect this change in altitude?
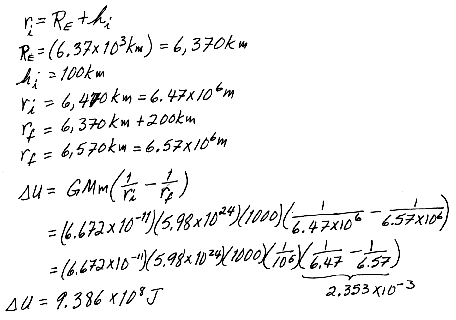
14.34 (a) What is the minimum speed necessary for a spacecraft to escape the Solar System, starting at Earth's orbit?
(b) Voyager I achieved a maximum speed of 125 000 km/h on its way to photograph Jupiter. Beyond what distance from the Sun is this speed sufficient to escape the Solar System?

14.57 In introductory Physics laboratories, a typical Cavendish balance for measuring the gravitational constant G uses lead spheres of masses 1.50 kg and 15.0 g whos centers are separated by 4.50 cm. Calculate the gravitational force between these spheres, treating each as a point mass located at the center of the sphere.

Solutions to the additional problems from Serway's fourth edition
(4 ed) 14.1 If the mass of Mars is 0.107 ME and its radius is 0.53 RE, estimate the gravitational field g at the surface of Mars.
(4 ed) 14.2 Geosynchronos satellites orbit Earth with a radius of about 42 000 km. This gives them the appropriate rotational speed wrt Earth so they appear stationary in the sky. What is the force on a 1 000-kg satellite at this height?
(4 ed) 14.3 How much energy is required to move a 1 000-kg mass from Earth's surface to an altidue of h = 2 RE?
| Hmwk, Ch 13 | Homework Assignments | PHY 1350's Home | Hmwk, Ch 15 |
(c) Doug Davis, 2001; all rights reserved