Ch4: 2, 5, 13, 17, 29, 37, 39, 47, 55, 65, 66
Questions 1, 4, 8, 13, 17, 30
Additional problems from Serway's fourth edition
Find the following:
(a) the time the ball is in flight,
(b) its initial velocity, and
(c) the x and y components of velocity just before the ball strikes the ground.
(4 ed) 4.4 A tire 0.500 m in radius rotates at a constant rate of 200 rev/min (rpm). Find the speed and acceleration of a small stone lodged in the tread on the outer edge of the tire.
When the particle reaches its maximum y coordinate, its y component of velocity is zero.
At this instant, find
(a) the velocity of the particle and
(b) its x and y coordinates.
Find the following:
(a) Santa's velocity components when he reaches the snow bank,
(b) the total time he is in motion, and(c) the distance d between the house and the point where he lands in the snow.
Conceptual Questions
Q4.1 Can an object accelerte if its speed is constant? Can an object accelerate if its velocity is constant?
Acceleration is the change in velocity divided by the change in time. So if the velocity is constant the change in velocity is zero and the acceleration is zero. However, the direction of the velocity can change even if its magnitude -- the speed -- is constant. Uniform Circular Motion (UCM) is a good example of nonzero acceleration with constant speed.
Q4.4 Describe a situation in which the velocity of a particle is always perpendicular to the position vector.
Uniform Circular Motion (UCM) is a good example of this:
Q4.8 A rock is dropped at the same instant that a ball at the same initial elevation is thrown horizontally. Which will have the greater speed when it reaches ground level?
They will both have the same vertical velocity component. However the one thrown horizontally will also have a horizontal velocity component. Therefore, the rock thrown horizontally will have the greater speed.
Q4.13 At the end of its arc, the velocity of a pendulum is zero. Is it acceleration also zero at this point?
No! If its acceleration were zero then its velocity would remain zero and it would just stop, suspended in mid-air. Just before it stopped, the pendulum's velocity was in one direction and a moment later its velocity will be in the opposite direction.
Q4.17 A baseball is thrown with an initial velocity of (10 i + 15 j) m/s. When it reaches the top of its trajectory, what are
(a) its velocity and
At the top, its vertical velocity component is zero. Throughout its flight, the horizontal velocity component remains constant. Therefore, its total velocity at the top is
vtop = ( 10 i + 0 j) m/s
vtop = ( 10 i ) m/s
(b) its acceleration?
Throughout the flight, the acceleration remains constant,
a = g = - (9.8 m/s2) j
Neglect air resistance
Q4.20 A projectile is fired at an angle of 30o from the horizontal with some initial speed. Firing at what other projectile angle results in the same range if the initial speed is the same in both cases? Neglect air resistance.
Any angle and 90o minus that angle have the same range. Therefore, the range is the same for 30o and for 60o.
Problems from the current (5th) edition of Serway and Beichner.
4.2 Suppose that the position vector for a particle is given asr(t) = x(t) i + y(t) j with x(t) = a t + b and y(t) = ct2 + d, where a = 1.00 m/s, b = 1.00 m, c = 0.125 m/s2, and d = 1.00 m.
(a) Calculate the average velocity during the time interval from t = 2.00 s to t = 4.00 s.
vavg =r /
r(4 s) = x(4 s) i + y(4 s) j
r(4 s) = [ a (4 ) + b ] i + [ c (4)2 + d ] j
r(4 s) = [ (1) (4) + 1 ] i + [ (0.125) (4)2 + 1 ] j
r(4 s) = [ 5 ] i + [ 3 ] j
r(2 s) = x(2 s) i + y(2 s) j
r(2 s) = [ a (2 ) + b ] i + [ c (2)2 + d ] j
r(2 s) = [ (1) (2) + 1 ] i + [ (0.125) (2)2 + 1 ] j
r(4 s) = [ 3 ] i + [ 1.5 ] j
vavg =
vavg = [2 i + 1.5 j ] m / 2 s
vavg = ( 1 i + 0.75 j ) m/s
(b) Determine the velocity and the speed at t = 2.00 s.
v = dr / dt = [ dx / dt ] i + [ dy / dt ] jv = [ d( a t + b) / dt ] i + [ d( ct2 + d ) / dt ] j
v = a i + 2 c t j
v = 1 i + (2) (0.125) (2) j
v = i + 0.5 j
v = ( i + 0.5 j ) m/s for t = 2 s
v = SQRT[ vx2 + vy2 ] = SQRT[ (1)2 + (0.5)2] m/s = SQRT[ 1.25 ] m/s = 1.12 m/s
4.5 At t = 0, a particle moving in the xy plane with constant acceleration has a velocity ofvo = (3 i - 2 j) m/s at the origin (i.e., ro = 0). At t = 3 s, its velocity is given by v = (9 i + 7 j) m/s. Find
(a) the acceleration of the particle and
a =
a =
a = [ 2 i + 3j ] m / s2
(b) its coordinates at any time t.
r = ro + vo t + 1 / 2 a t2r = [ 0 i + 0 j ] + [ 3 i - 2 j ] t + 1/2 [ 2 i + 3j ] t2
r = [ [ 3 t + t2 ] i + [ - 2 t + (3/2) t2 ] j ] m
x = ( 3 t + t2 ) m
y = [ - 2 t + (3/2) t2 ] m
4.13 An artillery shell is fired with an initial velocity of 300 m/s at 55.0o above the horizontal. It explodes on a mountainside 42.0 s after firing. What are the x and y coordinates of the shell where it explodes, relative to its firing point?
vx = v cos
= (300 m/s) cos 55o
vx = (300 m/s) (0,574) = 172,1 m/s
vy = v sin
vy = (300 m/s) (0,819) = 245.7 m/s
For motion with constant acceleration, we know
s = so + vo t + (1/2) a t2
Along the horizontal, x-axis, we might write this as
x = xo + vxo t + (1/2) ax t2
Measuring distances relative to the firing point means
xo = 0
We know that
ax = 0
or
vx = vxo = constant
vx = 172.1 m/s
x = (172.1 m/s) (42 s)
x = 72 282 m = 72.3 km
Along the vertical, y-axis, we might write this as
y = yo + vyo t + (1/2) ay t2
Measuring distances relative to the firing point means
yo = 0
We know that
ay = - g = - 9.8 m/s2
y = 0 + (245.7 m/s) t - (1/2) (9.8 m/s2) t2
y = 0 + (245.7 m/s) (42 s) - (1/2) (9.8 m/s2) (42 s)2
y = 1 675.8 m
4.17 A cannon with a muzzle speed of 1 000 m/s is used to start an avalanche on a mountain slope. The target is 2 000 m from the cannon horizontally and 800 m above the cannon. At what angle, above the horizontal, should the cannon be fired?
vx = v cos
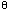
vx = (1 000 m/s) cos
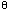
vy = v sin
voy = (1 000 m/s) sin
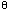
ax = 0
vx = constant
x = vx t
ay = - g = - 9.8 m/s2
y = yo + vyo t + (1/2) ay t2
y =vyo t - (1/2) g t2
y = [(1 000 m/s) sin
y = [(1 000) sin
t = x / vx
t = 2 000 m /[(1 000 m/s) cos
t = 2 000/[(1 000) cos
t = 2/cos
y = [(1 000) sin
y = [(1 000) sin
] (2/cos
y = [(2 000) (sin
800 = [(2 000) (sin
800 cos2
19.6 + 800 cos2
19.6 + 800 cos2
Now square both sides for
384 + 31 360 cos2
4 640 000 cos4
cos2
cos
This was a rather messy quadratic equation! But the whole problem was fairly straightforward. Just a bit messy with the unusually large numbers. But that's okay!
4.29 Young David, who slew Goliath, experimented with slings before tackling the giant. He found that with a sling of length 0.60 m, he could revolve the sling at the rate of 8.0 rev/s (Wow! that's really fast!). If he increased the length to 0.90 m, he could revolve the sling only 6.0 times per second.(a) Which rate of rotation gives the larger linear speed?
v = r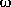
v6 = (0.6 m) (8 rev/s) ( 2
/ rev) = 30.16 m/s
v9 = (0.9 m) (6 rev/s) ( 2
Rotating it with a radius of 0.90 m and an angular velocity of 6 rev/s gives the greater linear speed.
(b) What is the centripetal acceleration at 8.0 rev/s?
ac = v2/rac = (30.16 m/s)2 / 0.6 m
ac = 1 516 m/s2
(c) What is the centripetal acceleration at 6.0 rev/s?
ac = v2/rac = (33.93 m/s)2 / 0.9 m
ac = 1 279 m/s2
4.37 A river has a steady speed of 0.50 m/s. A student swims upstream ad istance of 1.0 km and swims back to the starting point. If the student can swim at a speed of 1.2 m/s in still water, how long does the trip take? Compare this with the time the trip would take if the water were still.
vupstream = (1.2 - 0.5) m/s = 0.7 m/s
tupstream = 1 000 m / (0.7 m/s) = 1 429 s
vdownstream = (1.2 + 0.5) m/s = 1.7 m/s
tdownstream = 1 000 m / (1.7 m/s) = 588 s
ttotal = 1 429 s + 588 s = 2 017 s
Now, if the trip were done in still water we would simply have
tstill = 2 000 m / (1.2 m/s) = 1 667 s
4.39 The pilot of an airplane notes that the compass indicates a heading due west. The airplane's speed relative to the air is 150 km/h. If there is a wind of 30.0 km/h toward the north, find the velocity of the airplane relative to the ground.
Vpe = velocity of plane wrt earth
Vpa = velocity of plane wrt air
Vae = velocity of air wrt earth
Vpe is the hypotenuse of a right triangle, so we can readily find its magnitude by
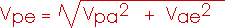
Now we need the direction of the velocity Vpe, the velocity of the plane with respect to (wrt) the earth. We have often measured directions relative to the x-axis. So we could specify the angle
shown in the diagram here.
However, directions in aviation are usually given relative to North. So we will find the angle
tan
Or, we might be quite specific and state
vpe = 153 km/h at 78.7o West of North
4.47 A projectile is fired up an incline (with incline angle
(a) Show that the projectile travels a distance d up the incline, where
d = [ 2 vi2 cos
(b) For what value of
Some may consider trig an art form in its own right. But Physicists -- and other scientists and engineers -- view trig -- and math in gen'l -- as a very useful tool. The Physics of this problem is not difficult. But it soon becomes a rather involved trig problem.
Now that we have an expression for d, we can find the maximum value of d by taking the derivative wrt angle
Can we check this answer? Well, maybe or just a little. When the incline angle
Rmax = v2/g
and that is the value or expression we expect.
4.55 A boy can throw a ball a maximum horizontal distance of 40.0 m on a level field. How far can he throw the same ball vertically upward? Assume that his muscles give the ball the same speed in each case.
We have derived the Range Equation,Xmax = vo2 sin 2
/ g
This range has its maximum value (Xmax,max?) for
Xmax,max = vo2 sin (2 x 45o) / g = vo2 / g = vo2 / (9.8 m/s2) = 40 m
vo2 = (9.8 m/s2) (40 m) = 392 m2 / s2
vo = 19.8 m / s
With this initial speed, what is the maximum height possible?
In the text, the maximum height equation is developed, Equation 4.17, on page 79,
h = vo2 sin2
Of course, this has its maximum value for
h max= vo2 / 2 g
h max= (19.8 m / s)2 / 2 (9.8 m/s2)
h max= 20 m
4.65 A car is parked on a steep incline overlooking the ocean, where the incline makes an angle of 37o below the horizontal. The negligent driver leaves the car in neutral and the parking brakes are defective. The car rolls from rest down the incline with a constant acceleration of 4.0 m/s2, traveling 50.0 m to the edge of a vertical cliff. The cliff is 30.0 m above the ocean.
Find
(a) the speed of the car when it reaches the edge of the cliff and the time it takes to get there.
(b) the velocity of the car when it lands in the ocean,
(c) the total time the car is in motion, and
(d) the position of the car when it lands in the ocean, relative to the base of the cliff.
(a) the speed of the car when it reaches the edge of the cliff and the time it takes to get there.
This is straight-line motion with constant acceleration:
v2 = vo2 + 2 a s
v2 = 0 + 2 (4.0 m/s2) (50 m)
v2 = 400 m2/s2
v = 20 m/s
With an acceleration of 4.0 m/s2, how long does it take to go from rest to 20 m/s?
v = vo + a t
20 m/s = 0 + (4.0 m/s2) t
t = 5 s
(b) the velocity of the car when it lands in the ocean,
How long is the car in the air after leaving the cliff, before it hits the ocean?
y = yo + vyo t + (1/2) ay t2
y = yo + vyo t - (1/2) g t2
0 = 30 m + ( - 12 m/s) t - (1/2) (9.8 m/s2) t2
Check the units. That is, do a dimensional analysis of this equation. Every term is a distance, measured in m. That's good. That give us confidence that the equation is correct (of course, that does not guarantee that it is correct). If we measure time t in units of seconds, then every term has only the unit of m in it and we can divide by that to have
0 = 30 - 12 t - 4.9 t2
4.9 t2 + 12 t - 30 = 0
t = 1.53 s
If we used the very reasonable approximation that g = 10 m/s2, this would be t = 1.5 s. In either case, there is also a solution for t < 0. While that satisfies the mathematics, it clearly does not satisfy the physics. Negative times are simply extraneous solutions.
Now, after falling for t = 1.53 s, what is the car's vertical velocity component?
vy = vyo + ay t
vy = - 12 m/s + ( - 9.8 m/s2) (1.53 s)
vy = - 27 m/s
Remember, of course, that the negative sign means it is falling down.
The horizontal component of the velocity remains constant,
vx = 16 m/s
v = SQRT (vx2 + vy2)
v = 31.4 m/s
That is the speed of the car. To find the velocity, we also need the direction,
tan
Notice that the "opposite side" was used as just 27, not - 27. This gives us the angle
(c) the total time the car is in motion,
Rolling down the incline took 5 s,
t1 = 5.0 s
It is in the air, falling from the edge of the cliff into the ocean, for 1.53 s,
t2 = 1.53 s
So the total time is just the sum of these two times,
ttot = 6.53 s
(d) the position of the car when it lands in the ocean, relative to the base of the cliff.
During this 1.53 s of free fall, the horizontal velocity remains constant a 16 m/s,
x = vx t
x = (16 m/s)(1.53 s)
x = 24.5 m
4.66 The determined Wyle E Coyote is out once more to try to capture the elusive Road Runner. The Coyote wears a pair of Acme jet-powered rollerblades, which provide a constant horizontal acceleration of 15.0 m/s2. See Figure P4.66. The Coyote starts off at rest 70.0 m from the edge of a cliff at the instant the RoadRunner zips past him in the direction of the cliff.
(a) If the RoadRunner moves with constant speed, determine the minimum speed he must have to reach the cliff before the Coyote.
At the brink of the cliff, the RoadRunner escapes by making a sudden turn, while the Coyote continues straight ahead.
(b) If the cliff is 100 m above the floor of a canyon, detemine where the Coyote lands in the canyon (assume his skates remain horizontal and continue to operate when he is in "flight").
(c) Determine the components of the Coyote's impact velocities.
[[ Yes, this, too, is long and involved; but I hope it is fun too! ]]
Please do this on your own and look at this solution only after you have done it yourself!
(a) If the RoadRunner moves with constant speed, determine the minimum speed he must have to reach the cliff before the Coyote.
Since we know the Coyote's acceleration, we can find his speed at the edge of the cliff and then the amount of time req'd to reach that speed,
v2 = vo2 + 2 a s
v2 = 0 + 2 (15.0 m/s2) (70 m)
v2 = 2100 m2/s2
v = 45.8 m/s
With an acceleration of 15.0 m/s2, how long does it take the Coyote go from rest to 45.8 m/s?
v = vo + a t
45.8 m/s = 0 + (15.0 m/s2) t
t = 3.05 s
This means the Road Runner has 3.05 s to travel this distance of 70.0 m,
vRR = 70 m/3.05 s
vRR = 22.9 m/s
(b) If the cliff is 100 m above the floor of a canyon, detemine where the Coyote lands in the canyon (assume his skates remain horizontal and continue to operate when he is in "flight").
How long is the Coyote in the air before smacking into the canyon floor? His initial vertical velocity is zero, vyo= 0, so his vertical motion is ordinary free fall,
y = yo + vyo t + (1/2) ay t2
y = yo + vyo t - (1/2) g t2
0 = 100 m + 0 - (1/2) (9.8 m/s2) t2
A quick check of units -- or dimensional analysis -- shows us that each term in this equation is a distance and if we measure time t in seconds we can write this equations as
0 = 100 + 0 - 4.9 t2
4.9 t2 = 100
t2 = 20.41
t = 4.52 s
How far does the Coyote move horizontally during this 4.52 s? He leaves the cliff with an initial horizontal velocity of vxo = 45.8 m/s and continues to have a horizontal acceleration of ax = 12 m/s2 during this 4.52 s,
x = xo + vxo t + (1/2) ax t2
x = 0 + (45.8 m/s)(4.53 s) + (1/2)(12 m/s2)(4.53 s)2
x = 330.6 m
(c) Determine the components of the Coyote's impact velocities.
vx = vxo + ax t
vx = 45.8 m/s + (12 m/s2)(4.53 s)
vx = 100 m/s
vy = vyo + ay t
vy = vyo - g t
vy = 0 - (9.8 m/s2)(4.53 s)
vy = - 44.4 m/s
Solutions to additional problems from Serway's fourth edition.
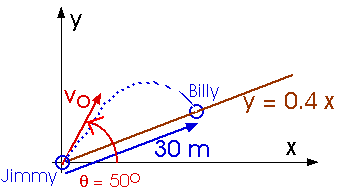
(4 ed) 4.1 Jimmy is at the base of a hill, while Billy is 30 m up the hill. Jimmy is at the origin of an xy coordinate system, and the line that follows the slope of the hill is given by the equation, y = 0.4 x, as shown in Figure P4.10. If Jimmy throws an apple to Billy at an angle of 50o with respect to the horizontal, with what speed must he throw the apple if it is to reach Billy?
vyo = vo sin 50o = 0.766 vo
For the hill,
rBilly = 30 m
xBilly = (30 m) (cos 21.8o) = (30 m)(0.928) = 27.85 m
yBilly = (30 m) (sin 21.8o) = (30 m)(0.371) = 11.14 m
xapple = vxo t
yapple = vyo t + (1/2) ay t2 = vyo t - (1/2) g t2
For some time t, we require xapple = xBilly and yapple = yBilly
xapple = xBilly
vxo t = 27.85 m
0.643 vo t = 27.85 m
t = (27.85 m) / (0.643 vo)
t = 43.31 / vo
Now we use this value of the time in
yapple = yBilly
vyo t - (1/2) g t2 = 11.14 m
[ 0.766 vo] [ 43.31 / vo ] - (1/2) [ 9.8 ] [ 43.31 / vo ]2 = 11.14
[ 0.766 vo] [ 43.31 / vo ] - (1/2) [ 9.8 ] [ 43.31 / vo ]2 = 11.14
33.18 - 9191 / vo2 = 11.14
9191 / vo2 = 22.04
vo2 = 9191 / 22.04 = 417
vo = 20.4 m/s
vo = 20.4 m/s
Now, let's check this to ensure it is correct:
t = 43.31 / vo = (43.31 / 20.4) s = 2.12 s
xapple = vxo t = 0.643 vo t = (0.643) (20.4 m/s) (2.12 s) = 27.8 m = xBilly
yapple = vyo t - (1/2) g t2 = 0.766 vo t - (1/2) (9.8) t2 = ? = yBilly
yapple = (0.766) (20.4) (2.12) - (1/2) (9.8) (2.12)2 =
= 33.16 - 22.02 = 11.1 m = yBilly
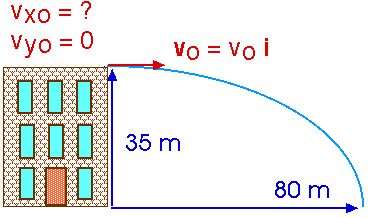
(4 ed) 4.2 A ball is thrown horizontally from the top of a building 35 m high. The ball strikes the ground at a point 80 m from the base of the building.Find the following:
(a) the time the ball is in flight,
y = yo + vyo t + (1/2) ay t2We are free to choose the origin of or coordinate system wherever we want. This time, let's choose the base of the building, so yo = 35 m and yf = 0.
y = 35 + 0 + (1/2) ( - g) t2
y = 35 + 0 - 4.9 t2 = 0 = yf
4.9 t2 = 35
t2 = 7.14
t = 2.67 s
(b) its initial velocity, and
x = xo + vxo t80 m = 0 + vxo (2.67 s)
vxo = 80 m / 2.67 s
vxo = 29.9 m/s
(c) the x and y components of velocity just before the ball strikes the ground.
vx = vxo = 29.9 m/s = constantvy = vyo + ay t
vy = 0 + ( - 9.8 m/s2 ) ( 2.67 s )
vy = - 26.2 m/s
(4 ed) 4.3 Superman is flying at treetop level near Paris when he sees the Eiffel Tower elevator start to fall (the cable snapped). His x-ray vision tells him Lois Lane is inside. If Superman is 1.00 km away from the tower and the elevator falls from a height of 240 m, how long does have to save Lois, and what must his average speed be?y = yo + vyo t + (1/2) ay t2We are also free to choose the direction of the positive y-axis. This time, since everything happens going down, let's choose down as positive. Then ay = g = 9.8 m/s2 and the ground is located at y = 240 m from the initial position of the elevator, yo = 0.
y = 0 + 0 t + (1/2) ( 9.8 ) t2 = 240 m
4.9 t2 = 240
t2 = 49.98
t = 7.0 s
That is how long the elevator falls before hitting the ground. During that time, Superman must travel 1.00 km = 1 000 m; therefore, his average speed must be
v =
v = 143 m/s
We could change this speed to km / hr for a better understanding of how fast this is,
v = 143 m /s [ km / 1 000 m ] [ 3 600 s / h ] = 514 km/h
514 km/h is 314 mi/h
(4 ed) 4.4 A tire 0.500 m in radius rotates at a constant rate of 200 rev/min (rpm). Find the speed and acceleration of a small stone lodged in the tread on the outer edge of the tire.
v = r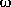v = r
ac = v2 / r
ac = ( 10.5 m/s )2 / 0.500 m
ac = 220.5 m / s2
(4 ed) 4.5 At t = 0 a particle leaves the origin with a velocity of 6.00 m/s in the positive y direction. Its acceleration is given bya = ( 2.00 i - 3.00 j ) m/s2 When the particle reaches its maximum y coordinate, its y component of velocity is zero.
At this instant, find
(a) the velocity of the particle and
vo = 6.00 j m/svxo = 0
vyo = 6.00 m/s
ro = 0
vy = vyo + ay t
vy = 6 + ( - 3 ) t = 0
t = 2 s
vx = vxo + ax t
vx = 0 + (2 m/s2 ) (2 s) = 4 m/s
(b) its x and y coordinates.
x = xo + vxo t + (1/2) ax t2x = 0 + 0 + (1/2) (2 m/s2) (2 s)2
x = 4 m
y = yo + vyo t + (1/2) ay t2
y = 0 + (6 m/s) (2 s) + (1/2) ( - 3 m/s2) (2 s)2
y = 6 m
(4 ed) 4.6 A football is thrown toward a receiver with an initial speed of 20.0 m/s at an angle of 30.0o above the horizontal. At that instant, the receiver is 20.0 m from the quaterback. In what direction and with what constant speed should the receiver run in order to catch the football at the level at which it was thrown?
Where is the football going? That is, how far does it move horizontally by the time it gets back to the vertical level at which it was thrown? We need the initial components of the velocity (or the components of the initial velocity).vxo = vo cos
vyo = vo sin
Set y = yo + vyo t - (1/2) g t2 = yo
vyo t - (1/2) g t2 = 0
[ vyo - (1/2) g t ] t = 0
Either t = 0, which is "true" but "uninteresting", or
t = 2 vyo / g
t = 2 ( 10.00 m/s ) / (9.8 m/s2 )
t = 2.04 s
Now we know how long the football is in the air. How far does it travel in this time?
x = vxo t
x = (17.32 m/s ) (2.04 s)
x = 35.3 m
At the time the quarterback throws the football, the receiver is 20 m away. During the next 2.04 s, he must run away from the quarterback to get to a distance of 35.3 m when the football arrives. The receiver is already 20 m away so he must run an additional 15.3 m in that time of 2.04 s. Therefore he needs to run with a constant (or average) speed of
v = 15.3 m / 2.04 s
v = 7.50 m/s
(4 ed) 4.7 After delivering his toys in the usual manner, Santa decides to have some fun and slide down an icy roof, as in Figure P4.78. He starts from rest at the top of the roof, which is 8.00 m in length, and accelerates at the rate of 5.00 m/s2. The edge of the roof is 6.00 m above a soft snow bank, which Santa lands on.Find the following:
(a) Santa's velocity components when he reaches the snow bank,
While sliding along the icy roof for 8.00 m, Santa's acceleration, we are told, is 5.00 m/s2For this motion along a straight line, we can use
v2 = vo2 + 2 a ( s - so )
v2 = 0 + 2 ( 5 m/s2 ) ( 8 m )
v2 = 80 m2/s2
v = 8.94 m/s
This is Santa's speed at the eave of the roof; call this v1.
v1 = 8.94 m/s
The roof is inclined 37o, so
vx1 = v1 cos 37o = (8.94 m/s) (0.80) = 7.16 m/s
vy1 = - v1 sin 37o = - (8.94 m/s) (0.60) = - 5.37 m/s
Santa reaches the snow bank 6.00 m below this point. Call this point x1 = 0, y1 = 6.0 m and then Santa reaches the snow bank at y = 0. How long does this take? For what value of the time t does y = 0?
y = y1 + vy1 t + (1/2) (- g) t2 = 0
6.0 m - (5.37 m/s) t - (4.9 m/s2) t2 = 0
6.0 - 5.37 t - 4.9 t2 = 0
4.9 t2 + 5.37 t - 6.0 = 0
Now we use the quadratic equation and find
t1 = 0.69 s
t2 = - 1.78 s
Of course, we are interested only in the positive value,
t = 0.69 s
vy = vy1 + ay t
vy= - 5.37 m/s - 9.8 m/s2 (0.69 s)
vy = - 12.13 m/s
vx = vx1 = 7.16 m/s = constant
(b) the total time he is in motion, and
To slide down the icy roof requires time troof. In finding Santa's speed as he comes off the roof, we did not find this time. We can find it now fromv = vo + a t
8.94 m/s = 0 + (5.0 m/s2) t
t = troof = 1.79 s
And we just found that Santa is airborne for an additional time of tair
tair = 0.69 s
ttot = troof + tair = 2.48 s
(c) the distance d between the house and the point where he lands in the snow.
Once he leaves the roof, Santa's horizontal speed remains constant,x = vxo t
x = (7.16 m/s) (0.69 s)
x = 4.9 m
| Hmwk, Ch 3 | Homework Assignment Page | PHY 1350's Home Page | Hmwk, Ch 5 | (c) Doug Davis, 2001; all rights reserved
