

Homework
Ch 2, Motion in One Dimension
Ch 2: 4, 9, 12, 14, 19, 21, 29, 39, 40
Questions 4, 5, 6, 9, 16
| Homework Assignment Page | PHY 1350's Home Page | Hmwk, Ch 3 |
Additional problems from Serway's fourth edition
(4 ed) 2.1 The position-time graph for a particle moving along the z-axis is as shown in an old Figure P2.1. Determine whether the velocity is positive, negative, or zero at times t1, t2, t3, and t4
(4 ed) 2.2 The new BMW M3 can accelerate from zero to 60 mi/h in 5.6 s
(a) What is the resulting acceleration in m/s2?
(b) How long would it take the BMW to go from 60 mi/h to 130 mi/h at this rate?
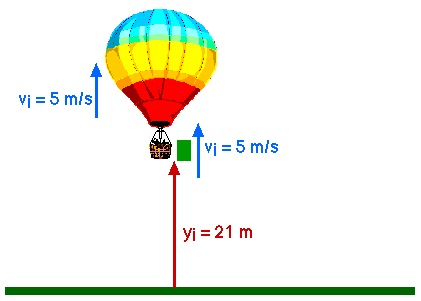
(4 ed) 2.3 A hot air balloon is traveling vertically upward at a constant speed of 5.00 m/s. When it is 21.0 m above the ground, a package is released from the balloon.
(a) After it is released, for how long is the package in the air?
(b) What is its velocity just before impact with the ground!
(c) Repeat (a)and (b) for the case of the baloon descending at 5.0 m/s.
(4 ed) 2.4 A hockey player is standing on his skates on a frozen pond when an opposing player skates by with the puck, moving with a uniform speed of 12.0 m/s. After 3.00 s, the first player makes up his mind to chase his opponent. If the first player accelerates uniformly at 4.00 m/s2,
(a) how long does it take him to catch the opponent?
(b) How far has the first player traveled in this time?
Conceptual Questions
2.Q4 Is it possible to have a situation in which the velocity and acceleration have opposite signs? If so, sketch a velocity-time graph to prove your point.
Certainly. Consider a car moving to the right but slowing down. Moving to the right means its velocity is positive. Slowing down means its velocity is decreasing or the change in velocity is negative and that means the acceleration is negative.
2.Q5 If the velocity of a particle is nonzero, can its acceleration be zero? Explain.
If the velocity is constant the acceleration is zero.
2.Q6 If the velocity of a particle is zero, can its acceleration be nonzero? Explain.
A velocity of zero is also a constant velocity and that means the acceleration is zero.
2.Q9 A student at the top of a building of height h throws one ball upward with an initial speed vyi and then throws a second ball downward wit the same initial speed. How do the final speeds of the balls compare when they reach the ground?
This one will be fun or interesting to talk about again after we have studied Energy Conservation.
When the ball that was initially thrown upward comes back to the height of the top of the building, its speed is again vyi. It will have the same speed. Of course its velocity will be - vyi because it is moving down. That means that it has exactly the same speed and velocity at the ball that is initially thrown downward with initial speed vyi so the two balls hit the ground with exactly the same speed (and velocity!).
2.Q16 A pebble is dropped into a water well and the splash is heard sixteen seconds later; as illustrated in the "BC" cartoon in Figure !2.16. Estimate the distance from the top of the well to the water's surface.
We can use the equation
y = yi + vyi + (1/2) ay t2
We are measuring distances from the top of the well so yi = 0 and we drop the pebble so vyi = 0 so this equation reduces to
y = (1/2) ay t2
y = (1/2) ( - 9.8 m/s2 ) (16 s)2
y = - 1 254.4 m
That is a very deep "well", indeed! But, maybe, wells were deeper in such prehistoric times. If we had used the approximation that ay = - g = - 10 m/s2, then our value would have been
y = - 1 280 m
Problems from the current (5th) edition of Serway and Beichner.
2.4 A particle moves according to the equation x = 10 t2 where x is in meters and t is in seconds.
(a) Find the average velocity for the time interval from 2.0 s to 3.0 s.
x(2 s) = 10 (2)2 = 10 (4) = 40 mx(3 s) = 10 (3)2 = 10 (9) = 90 m
x = xf - xi = x(3 s) - x(2 s) = 90 m - 40 m = 50 m
t = 1.0 s
vavg =
x /
t = 50 m / 1.0 s = 50 m/s
(b) Find the average velocity for the time interval 2.0 s to 2.1 s
x(2 s) = 10 (2)2 = 10 (4) = 40 mx(2.1 s) = 10 (2.1)2 = 10 (4.41) = 44.1 m
x = xf - xi = x(2.1 s) - x(2 s) = 44.1 m - 40 m = 4.1 m
t = 0.1 s
vavg =
x /
t = 4.1 m / 0.1 s = 41 m/s
[[ (c) Find the instantaneous velocity at t = 2.0 s
v = dx/dt = dx/dt = 10 [ d(t2)/dt ] = 10 [ 2t ] = 20 tv(2 s) = 20 (2) = 40 m/s = 40 m/s ]]
2.9 The position-time graph for a particle moving along the x-axis is shown in Figure P2.9
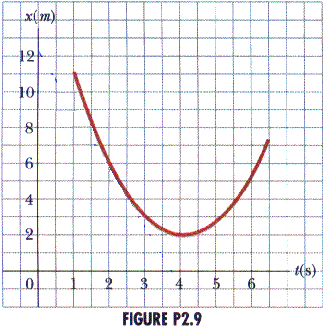
(a) Find the average velocity in the time interval t = 1.5 s to t = 4.0 s.
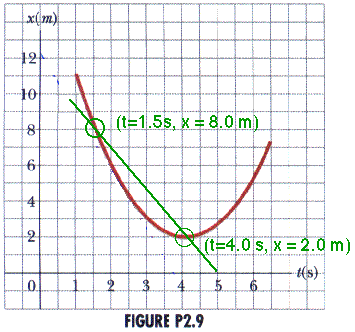 From the graph, we can findx (1.5 s) = 8 m
From the graph, we can findx (1.5 s) = 8 mand
x(4.0 s) = 2 m
x = xf - xi = x(4.0 s) - x(1.5 s) = 2 m - 8 m = - 6 m
t = tf - ti = 4.0 s - 1.5 s = 2.5 s
vavg =
x /
t = - 6 m / 2.5 s = - 24 m/s
Remember,
anything means (final value) - (initial value)
(b) Determine the instantaneous velocity at t = 2.0 s by measuring the slope of the tangent line shown in the graph.
To measure the slope of the line drawn tangent to the curve at t = 2.0 s, we can pick two points on the line.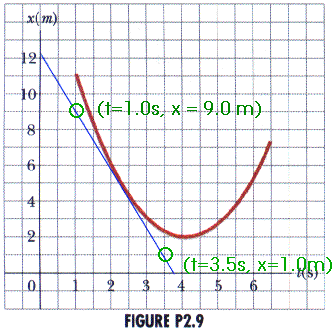
We might choose
(t = 1.0 s, x = 9.0 m)and
(t = 3.5 s, x = 1.0 m)Now we calculate v =
x /
t
x = xf - xi = 1.0 m - 9.0 m = - 8.0 m
t = tf - ti = 3.5 s - 1.0 s = 2.5 s
vavg =
x /
t = - 8.0 m / 2.5 s = - 32 m/s
(c) At what value of t is the velocity zero?
The velocity is zero when the slope of the tangent line (on an x-, t- graph) is zero.
That happens on this graph for t = 4.0 s .
2.12 A particle is moving with a velocity vo = 60.0 m/s in the positive x direction at t = 0. Between t = 0 and t = 15 s, the velocity decreases uniformly to zero. What is the average acceleration during this 15-s interval. What is the significance of the sign in your answer?
a =v /
t
v = vf - vi = vf - vo = 0 - 60 m/s = - 60 m/s
t = 15 s
a =
v /
t = [ - 60 m/s ] / [ 15 s ] = - 4 (m/s)/s = - 4 m/s2
The minus sign means the particle is slowing down. Its velocity is decreasing. It is decelerating.
2.14 A particle starts from rest and accelerates as shown in Figure P2.14.
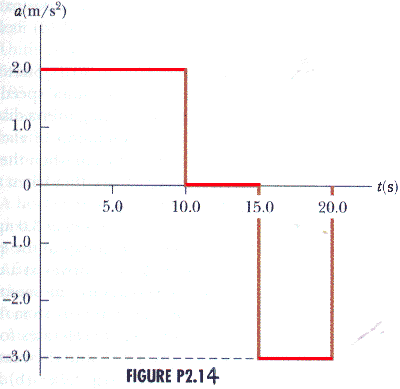
Determine the following:
(a) the particle's speed at t = 10 s and at t = 20 s and
From the graph, we can see that from t = 0 to t = 10 s, the acceleration is a constant 2.0 m/s2v = vi + a tvi = 0
a = 2 m/s2
v(10 s) = 0 + (2 m/s2) (10 s)
v(10 s) = 20 m/s
For the next five seconds, from t = 10 s to t = 15 s, the acceleration is zero which means the velocity remains constant,
v(15 s) = 20 m/sFor the next five seconds, from t = 15 s to t = 20 s, the acceleration is negative, a = - 3.0 m/s2
v = vi + a tvi = v(15 s) = 20 m/s
a = - 3 m/s2
v(20 s) = 20 m/s + (- 3 m/s2) (5 s)
v(20 s) = 5 m/s
(b) the distance traveled in the first 20 s
We have already determined the values of the acceleration for various time intervalsx = xi + vi t + (1/2) a t2xi = 0
vi = 0
a = 2 m/s2
x(10 s) = 0 + 0 + (1/2) (2 m/s2)(10 s)2
x(10 s) = 100 m
The acceleration remains constant (at a = 0) for the next five seconds (until t = 15 s) so we can, again, apply this equation which describes distance with constant acceleration.
x = xi + vi t + (1/2) a t2xi = x(10 s) = 100 m
vi = v(10 s) = 20 m/s
a = 0
x(15 s) = 100 m + (20 m/s)(5 s) + (1/2) (0)(5 s)2
x(10 s) = 200 m
The acceleration again remains constant (at a = - 3 m/s2) for the next five seconds (until t = 20 s) so we can, again, apply this equation which describes distance with constant acceleration.
x = xi + vi t + (1/2) a t2xi = x(15 s) = 200 m
vi = v(15 s) = 20 m/s
a = - 3 m/s2
x(20 s) = 200 m + (20 m/s)(5 s) + (1/2) ( - 3 m/s2)(5 s)2
x(20 s) = 262.5 m
2.19 Figure P2.19 shows a graph of v versus t for the motion of a motocyclist as she starts from rest and moves along the road in a straight line.
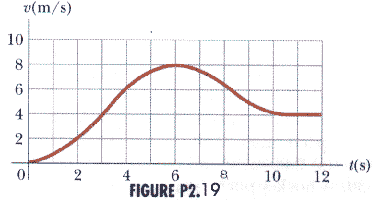
(a) Find the average acceleration for the time interval to = 0 to t1 = 6.0 s.
From the graph, we can read the velocities for these timesv1 = v(t1) = v(6 s) = 8 m/svo = v(to) = v(0 s) = 0
v = v1 - vo = 8 m/s - 0 = 8 m/s
t = 6.0 s
a =
v /
t = [8 m/s ] / [6 s] = 1.33 m/s2
a = 1.33 m/s2
(b) Estimate the time at which the acceleration has its greatest positive value and the value of the acceleration at this instant.
Acceleration is the slope of the line on a velocity-time graph like Figure P2.23. The slope seems greatest at aboutt = 3 sAnd, there, I estimate the slope by sketching a tangent line which goes through the points
(t = 1 s, v = 0) and (t = 6 s, v = 10 m/s)
v = vf - vi = 10 m/s - 0 = 10 m/s
t = 6.0 s
a =
v /
t = [10 m/s ] / [6 s] = 1.67 m/s2
a = 1.67 m/s2
(c) When is the acceleration zero?
Zero acceleration means the slope of the line tangent to the curve on a v-t graph is zero.a = 0 for t = 6 s(d) Estimate the maximum negative value of the acceleration and the time at which it occurs.
Acceleration is the slope of the line on a velocity-time graph like Figure P2.23. The slope is negative from t = 0 to about t = 10 seconds. During that time, the slope seems greatest (negatively) at about t = 8 s. T here, I estimate the slope by sketching a tangent line which goes through the points(t = 6 s, v = 10 m/s) and (t = 11 s, v = 0 m/s)
v = vf - vi = 0 m/s - 10 m/s = - 10 m/s
t = 5.0 s
a =
v /
t = [- 10 m/s ] / [5 s] = - 1.8 m/s2
a = - 1.8 m/s2
2.21 Jules Verne in 1865 proposed sending people to the Moon by firing a space capsule from a 220-m-long cannon with a final velocity of 10.97 km/s. What would have been the unrealistically large acceleration experienced by the space travelers during launch? Compare your answer with the free-fall acceleration of 9.8 m/s2.
First, let's change the final velocity to units of m/s; we can almost do that in our heads.
vf = 10.97 km/s [1000 m/km] = 10.97 x 103 m/s
2.29 A drag racer starts her car from rest and accelerates at 10.0 m/s2 for the entire distance of 400 m (1/4 mile).
(a) How long did it take the car to travel this distance?
x = xi + vi t + (1/2) a t2400 m = 0 + 0 + (1/2) (10 m/s2) t2
t2 = 80 s2
t = 8.94 s
(b) What is its speed at the end of the run?
v = vi + a tv = 0 + (10 m/s2)(8.94 s)
v = 89.4 m/s
v = 89.4 m/s [ 3600 s/h ] [ km/1000 m ] = 322 km/h
v = 322 km/h [ mi/1.61 km ] = 200 mi/h
2.39 A ball accelerates at 0.5 m/s2 while moving down an inclined plane 9.0 m long. When it reaches the bottom, the ball rolls up another plane, where, after moving 15 m, it comes to rest.
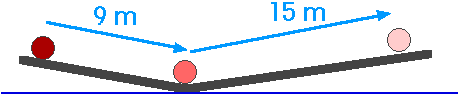
(a) What is the speed of the ball at the bottom of the first plane?
 v2 = vi2 + 2 a (x - xi)
v2 = vi2 + 2 a (x - xi)v2 = 02 + 2 (0.5 m/s2)(9 m) = 9 m2/s2
v = 3 m/s
(b) How long doe is take to roll down the first plane?
v = vi + a t3 m/s = 0 + (0.5 m/s2) t
t = 6 s
(c) What is the acceleration along the second plane?
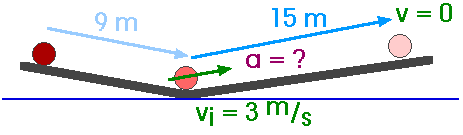 v2 = vi2 + 2 a (x - xi)
v2 = vi2 + 2 a (x - xi)What value of a brings the ball to rest, having
v = 0when it started with
vi = 3 m/safter traveling a distance of
x - xi = 15 mv2 = vi2 + 2 a (x - xi)
02 = (3 m/s)2 + 2 a (15 m)
a = - 0.3 m/s2
(d) What is the ball's speed 8.0 m along the second plane?
 v2 = vi2 + 2 a (x - xi)
v2 = vi2 + 2 a (x - xi)v2 = (3 m/s)2 + 2 ( - 0.3 m/s2) ( 8 m)
v2 = ( 9 - 4.8 ) (m2/s2) = 4.2 m2/s2
v = 2.05 m/s
2.40 Speedy Sue driving at 30 m/s enters a one-lane tunnel. She then observes a slow-moving van 155 m ahead traveling at 5.0 m/s. Sue applies her brakes but can decelerate only at 2.0 m/s2 because the road is wet. Will there be a collision?

If yes, determine how far into the tunnel and at what time the collision occurs.
If no, determine the distance of closest approache between Sue's car and the van.
We will measure distances from the tunnel's entrance.The position of the van is given by
xvan = xv = xvi + vvi t + (1/2) av t2xvi = 155 m
vvi = 5.0 m/s
av = 0
xv = 155 m + (5.0 m/s) t + 0
xv = 155 m + (5.0 m/s) t
The position of Speedy Sue's car is given by
xcar = xc = xci + vci t + (1/2) ac t2xci = 0
vci = 30.0 m/s
ac = - 2.0 m/s2
xc = 0 + (30 m/s) t + (1/2) (- 2.0 m/s2) t2
xc = (30 m/s) t + (1/2) (- 2.0 m/s2) t2
To determine if there is a collision, we can set these two positions equal to each other (as they will be if there is a collision) and solve for t, the time at which that collision occurs.
xc = xv(30 m/s) t + (1/2) (- 2.0 m/s2) t2 = 155 m + (5.0 m/s) t
(1 m/s2) t2 + ( - 25 m/s) t + 155 m = 0
This is now in the "standard form" of a quadratic equation,
a x2 + b x + c = 0with
x = ta = 1 m/s2
b = - 25 m/s
c = 155 m
So we can now use the quadratic equation to solve for t. We can explicitly keep the units or we can ensure that the units are consistent and simply write
a = 1, b = - 25, and c = 155
t = 11.4 seconds or t = 13.6 seconds
The collision occurs 11.4 seconds after entering the tunnel. Mathematically, t = 13.6 s is also a solution, but the collision has already occured about two seconds before that!
Solutions to the additional problems from Serway's fourth edition
(4 ed) 2.1 The position-time graph for a particle moving along the z-axis is as shown in an old Figure P2.14. Determine whether the velocity is positive, negative, or zero at times
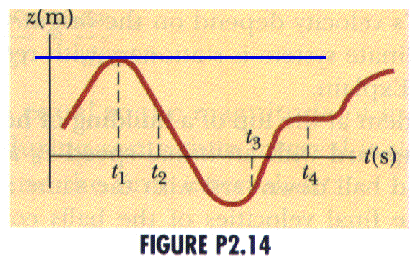
a) t1 ; the velocity, as the slope of the tangent line, is zero
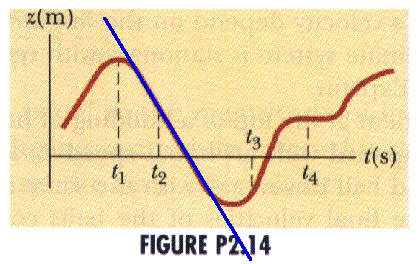
b) t2 ; the velocity, as the slope of the tangent line, is negative
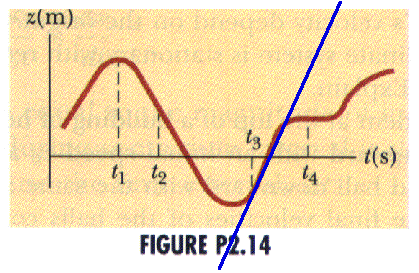
c) t3 ; the velocity, as the slope of the tangent line, is positive
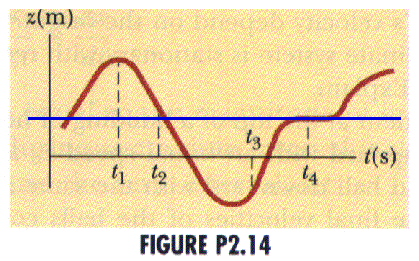
d) t4 ; the velocity, as the slope of the tangent line, is zero
(4 ed) 2.2 The new BMW M3 can accelerate from zero to 60 mi/h in 5.6 s
(a) What is the resulting acceleration in m/s2?
a =v /
t = [ 60 mi/h ] / 5.6 s = 10.7 (mi/h)/s
a = 10.7 mi/h/s
a = 10.7 mi/(h - s) [ 1.61 km/mi ] [ 1000 m/km ] [ h/3600 s] = 4.79 m/s2
a = 4.79 m/s2
(b) How long would it take the BMW to go from 60 mi/h to 130 mi/h at this rate?
v = vi + a ta t = v - vi
t = [v - vi] / a
t = [ 130 mi/h - 60 mi/h ] / (10.7 mi/h/s )
t = [ 70 mi/h ] / (10.7 mi/h/s )
t = 6.54 s
That is 6.45 seconds beyond the 5.6 s required to reach 60 mi/h. The total timewill be
ttot = 5.6 s + 6.54 sttot = 12.1 s
(4 ed) 2.3 A hot air balloon is traveling vertically upward at a constant speed of 5.00 m/s. When it is 21.0 m above the ground, a package is released from the balloon.

(a) After it is released, for how long is the package in the air?
Once released, the package is in free fall with an acceleration ofa = - g = - 9.8 m/s2We know its initial velocity and initial position
vi = 5 m/syi = 21 m
The later position of the package is given by
y = yi + vi t + (1/2) a t2y = 21 m + (5 m/s) t + (1/2) ( - 9.8 m/s2) t2
Now we set y = 0 and solve for t
y = 0 = 21 m + (5 m/s) t + (1/2) ( - 9.8 m/s2) t2As before, we can carry the units explicitly or we can ensure that we have consistent units and drop them and write only
4.9 t2 - 5 t - 21 = 0From the quadradic equation, we find the two solutions of t
t1 = 2.64 s, and t2 = - 1.62 sPhysically, we are only interested in solutions for t > 0. Mathematically, our equation is only valid for t > 0 since it is valid only after the package is released. So we use only t1.
t = 2.64 s(b) What is its velocity just before impact with the ground!
Once released, the velocity of the package is given byv = vi + a tv = 5 m/s + ( - 9.8 m/s2) t
v = 5 m/s + ( - 9.8 m/s2) (2.64 s)
v = - 20.9 m/s
Of course, the minus sign indicates that the velocity is directed downward.
(c) Repeat (a)and (b) for the case of the baloon descending at 5.0 m/s.
As before, once released, the package is in free fall with an acceleration ofa = - g = - 9.8 m/s2We know its initial velocity and initial position
vi = - 5 m/sThe package, along with the balloon, is now moving downward and this shows up as the negative sign on the velocity
yi = 21 mThe later position of the package is given by
y = yi + vi t + (1/2) a t2y = 21 m + ( - 5 m/s) t + (1/2) ( - 9.8 m/s2) t2
Now we set y = 0 and solve for t
y = 0 = 21 m + ( - 5 m/s) t + (1/2) ( - 9.8 m/s2) t2As before, we can carry the units explicitly or we can ensure that we have consistent units and drop them and write only
4.9 t2 + 5 t - 21 = 0From the quadradic equation, we find the two solutions of t
t1 = 1.62 s, and t2 = - 2.64 sPhysically, we are only interested in solutions for t > 0. Mathematically, our equation is only valid for t > 0 since it is valid only after the package is released. So we use only t1.
t = 1.62 sOnce released, the velocity of the package is given by
v = vi + a tv = - 5 m/s + ( - 9.8 m/s2) t
v = - 5 m/s + ( - 9.8 m/s2) (1.62 s)
v = - 20.9 m/s
Notice that the velocities are the same. Later on, we can describe this in terms of energy conservation. The kinetic energy of the package is the same whether it is thrown upwith v = + 5 m/s or if it is thrown down with v = - 5 m/s.
(4 ed) 2.4 A hockey player is standing on his skates on a frozen pond when an opposing player skates by with the puck, moving with a uniform speed of 12.0 m/s. After 3.00 s, the first player makes up his mind to chase his opponent. If the first player accelerates uniformly at 4.00 m/s2,
(a) how long does it take him to catch the opponent?
We know the initial velocities and accelerations of the two players,a1 = 4 m/s2, a2 = 0v1i = 0, v2i = 12 m/s
x1i = x2i = 0
The position of player #2 is given by
x2 = x2i + v2i t + (1/2) a2 t2x2 = (12 m/s) t
Be careful with the time. We must account for player #1's wait of 3 s. With this accounted for, we can calculate the position of player #1 from
x1 = x1i + v1i (t - 3 s) + (1/2) a1 (t - 3 s)2Of course, this equation only makes sense for t > 3 s.
x1 = 0 + 0 + (1/2) (4 m/s2) (t - 3 s)2 = (2 m/s2) (t2 - 6 s t + 9 s2)Now we set x1 = x2 and solve for the time t.
x1 = x2(2 m/s2) (t2 - 6 s t + 9 s2) = (12 m/s) t
We can either keep the units in explicitly or ensure that we have consistent units and simply write
2 (t2 - 6t + 9) = 12t2 t2 - 12 t + 18 = 12 t
2 t2 - 24 t + 18 = 0
t2 - 12 t + 9 = 0
There are two solutions to this quadratic equation,
t1 = 11.2 s, and t2 = 0.8 sHowever, the equation for the position of player #1 is not valid for t2 < 3 s, so we keep only tx,
t = 11.2 s(b) How far has the first player traveled in this time?
Now where is player #2 (and, therefore, player #1 as well) at this time?x2 = x2i + v2i t + (1/2) a2 t2x2 = (12 m/s) t
x2 = (12 m/s) (11.2 s)
x2 = 134.4 m
(Is a hockey rink that large?)
| Homework Assignment Page | PHY 1350's Home Page | Hmwk, Ch 3 | (c) Doug Davis, 2001; all rights reserved