PHY 1351
Third Hour Exam
(Wednesday) 7 November 2001

| Course Calendar |

Possibly useful information:


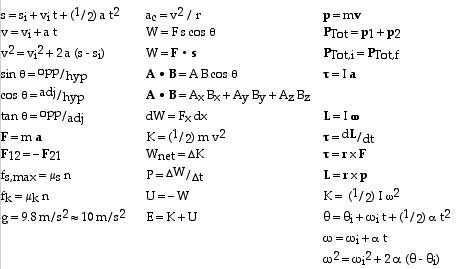
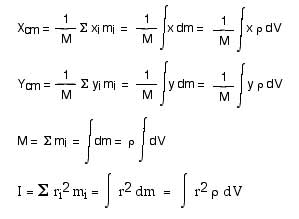
A x B = i (Ay Bz – Az By ) + j (Az Bx – Az Bz ) + k (Ax By – Ay Bx)
C = A x B; C = A B sin f
C is perpendicular to both A and B (The direction of C is determined by the right-hand rule).

The unit following a number is necessary!

We can use this to our advantage.

You can not add "apples" and "oranges". Three "apples" can never equal four "oranges".

Apples and oranges may be interchangeable on US postage stamps -- but you still can not add them!

Every term in an equation must have the same unit.

Conceptual Questions: I think Conceptual Questions are important. However, we have covered a lot of material in these three chapters. I felt I could not ask less than five Calculational Questions and that simply left no time for Conceptual Questions! They will reappear on the final and, I expect, on the Fourth Hour Exam.
Again, as you know, we have covered many interesting and important topics. Time simply has not permited questions on rocket propulsion, calculating moments of inertia, and several other important ideas. Don’t be alarmed for I will try to get to them on the final exam. Physics is such a rich and diverse and interesting area!

| Course Calendar |

Calculational Questions:
1. In a particular crash test, an automobile of mass 1,500 kg collides with a wall. The initial and final velocities of the automobile are vi = – 15.0 i m/s and vf = + 2.6 i m/s. If the collision lasts for 0.150 s, find the impulse (or change in momentum) caused by the collision and the average force exerted on the automobile. This is Example 9.4 on page 258.

Impulse = change in momentum

Impulse = p = pf - pi

p = pf - pi = m vf - mvi

p = (1500 kg)(2.6 m/s) - (1500 kg)( - 15 m/s)

p = (1500 kg)(2.6 + 15)(m/s)

p = (1500 kg)(17.6)(m/s)

p = 26,400 kg-m/s

F = p/t

F = (26,400 kg-m/s) / (0.150 s)

F = 176,000 kg-m/s2

F = 176,000 N

F = 176 kN

F = 1.76 x 105 N

This force acts in the i-direction or the positive x-direction.

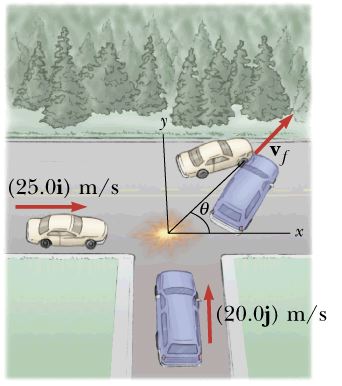
2. A 1,500-kg car traveling east with a speed of 25.0 m/s collides at an intersection with a 2,500-kg van traveling north at a speed of 20.0 m/s. Find the direction and magnitude of the velocity of the wreckage after the collision, assumeing that the vehicles undergo a perfectly inelastic collision (that is, they stick together). This is Example 9.9, from page 267.

Ptot,final = Ptot,init

Ptot,init = p1 + p2

Ptot,init = mcar vcar + mvan vvan

Ptot,init = (1500 kg)(25.0 i m/s) + (2500 kg)(20.0 j m/s)

Ptot,init = (37,500 kg-m/s) i + (50,000 kg-m/s) j

Ptot,final = Mtot vfinal

Ptot,final = (4,000 kg) vfinal

Ptot,final = Ptot,init

vfinal = [(37,500 kg-m/s) i + (50,000 kg-m/s) j ]/(4,000 kg)

vfinal = (9.375 m/s) i + (12.5 m/s) j

vfinal = SQRT[(9.375)2 + (12.5)2] m/s

vfinal = SQRT[87.89 + 156.25] m/s

vfinal = SQRT[244.14] m/s

vfinal = 15.6 m/s

tan = opp/adj = vy/vx

tan = 50,000 kg-m/s/37,500 kg-m/s

tan = 50/37.5 = 1.33

= 53o

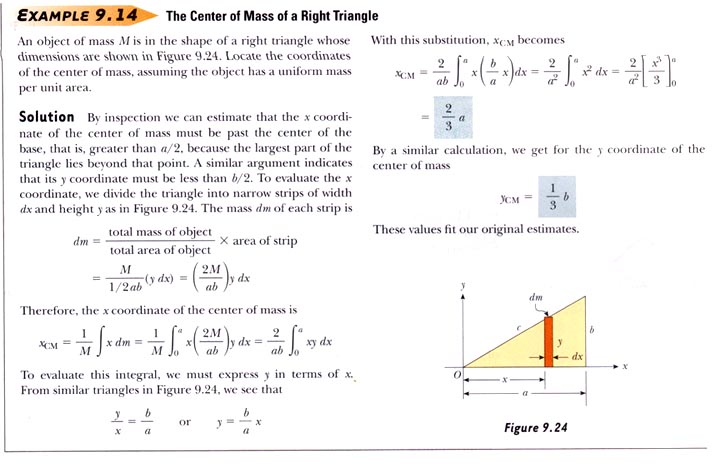
3. Show that the center of mass of a uniform right triangle of sides a and b is

Xcm = (1/3) a
Ycm = (1/3) b

That is, derive this result — using calculus.

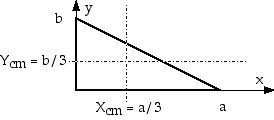
This is Example 9.14, from page 273.

Calculus is a very important "tool of the trade" for Engineers and Scientists!

Another double integral calculus question like this -- or, more probably, involving a moment of inertia -- will surely reappear on the final exam. Calculus is important!

4. A solid wheel has radius R = 0.10 m and mass M = 1.0 kg.

a) Calculate its moment of inertia from I = (1/2) M R2.

I = (1/2)(1.0 kg)(0.10 m)2

I = 0.005 kg-m2

This wheel is mounted on a frictionless, horizontal axis. A light cord wrapped around the wheel supports an object of mass m = 0.250 kg.

b) Calculate the angular acceleration of the wheel.

This is just a numerical version of Example 10.12 on page 310.

[[ Because of time constraints, this is all I am asking about this question. With more time, tho’, you could easily find the linear acceleration of the supported object and the tension in the cord. ]]

For the wheel,

= I

= (0.005 kg-m2)

= R T = (0.10 m) T

(0.10 m) T= (0.005 kg-m2)

That's well and good, of course, but we need add'l information since this one equation has two unknowns (the tension T and the angular acceleration ). We will get that add'l information by looking at the hanging object of mass m - 0.250 kg.

For the hanging object, I am taking "down" as positive,

Fnet = m g - T = m a

(0.250 kg)(9.8 m/s2) - T = (0.250 kg) a

Now we have two equations but we have three unknowns! The linear acceleration a and the angular acceleration are connected by

a = R

a = (0.10 m)

Now we can write

(0.250 kg)(9.8 m/s2) - T = (0.250 kg) (0.10 m)

And this does, indeed, give us two equations with two unknowns!

2.45 N - T = 0.025 kg-m

T = 2.45 N - 0.025 kg-m

Now, return to our earlier equation of

(0.10 m) T = (0.005 kg-m2)

(0.10 m) (2.45 N - 0.025 kg-m ) = (0.005 kg-m2)

0.245 N-m - 0.0025 kg-m2 = 0.005 kg-m2

0.245 N-m = 0.0075 kg-m2

0.0075 kg-m2 = 0.245 N-m

= (0.245 N-m)/(0.0075 kg-m2)

= 32.7 s - 2 = 32.7 (1/s2) = 32.7 rad/s2

That is all I asked for. But let's go ahead and find the linear acceleration and the tension.

a = R

a = (0.10 m)(32.7)(1/s2)

a = 3.27 m/s2

(0.250 kg)(9.8 m/s2) - T = (0.250 kg) a

(0.250 kg)(9.8 m/s2) - T = (0.250 kg) (3.27 m/s2)

2.45 N - T = 0.82 N

T = 2.45 N - 0.82 N

T = 1.63 N

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

5. A solid sphere, with moment of inertia Isph = (2/5) M R2, rolls down an inclined plane, as shown here, without slipping. What is the linear speed of the sphere at the bottom of the plane?.

– or – Answer the question above in terms of h, M and R or answer the question below numerically.

A solid sphere, with moment of inertia Isph = (2/5) M R2, with mass of M = 0.250 kg, and radius R = 0.05 m, rolls down an inclined plane, as shown here, from an initial height of h = 0.25 m, without slipping. What is the linear speed of the sphere at the bottom of the plane?

This is Example 11.1 on page 331.

Use Energy Conservation -- be be sure to include both translational kinetic energy and rotational kinetic energy.

Efinal = Einit

Einit = Ug = M g h

ie, Kinit = 0

Einit =M g h

Efinal = Ktrns + Krot

Efinal = (1/2) m v2 + (1/2) I 2

but

v = R

or

= v/R

Efinal = (1/2) m v2 + (1/2) I (v/R)2

Efinal = (1/2) m v2 + (1/2) (I/R2) v2

Efinal = (1/2) [ m + (I/R2)] v2

And for a solid sphere, I = (2/5) m R2, so we can write Efinal as

Efinal = (1/2) [ m + ((2/5) m R2/R2)] v2

Efinal = (1/2) [ (1 + 2/5) m ] v2

Efinal = (1/2) [ 7/5 m ] v2

Efinal = [ 7/10 m ] v2

Efinal = Einit

[ 7/10 m ] v2 = m g h

[ 7/10 ] v2 = g h

v2 = (10/7) g h

v = SQRT[(10/7) g h]

– or – We can answer the question numerically.

Use Energy Conservation -- be be sure to include both translational kinetic energy and rotational kinetic energy.

Efinal = Einit

Einit = Ug = m g h

ie, Kinit = 0

Einit = m g h = (0.250 kg)(9.8 m/s2)(0.25 m) = 0.6125 J

Efinal = Ktrns + Krot

Efinal = (1/2) M v2 + (1/2) I 2

Isph= (2/5) M R2 = (2/5) (0.250 kg) (0.05 m)2

Isph= 2.5 x 10 - 4 kg-m2

Efinal = (1/2) (0.250 kg) v2 + (1/2) (2.5 x 10 - 4 kg-m2) 2

but

v = R

or

= v/R

Efinal = (1/2) (0.250 kg) v2 + (1/2) (2.5 x 10 - 4 kg-m2) (v/R)2

Efinal = (1/2) (0.250 kg) v2 + (1/2) (2.5 x 10 - 4 kg-m2) (v/0.05 m)2

Efinal = (1/2) (0.250 kg) v2 + (1/2) (0.10 kg) (v)2

Efinal = (0.125 kg) v2 + (0.05 kg) v2

Efinal = (0.175 kg) v2

Efinal = Einit

Einit = 0.6125 J

0.175 kg v2 = 0.6125 J

v2 = (0.6125/0.175) (J/kg)

v2 = 3.5 (J/kg)

You already know that I think units are (very!) important. What is a "J/kg"? Let's see, . . .

J/kg = [ N m ]/kg

J/kg = [(kg m/s2) m]/kg

J/kg = m2/s2

Ant those are the units that v2 must have!

v = SQRT[3.5] m/s

v = 1.87

m/s

| Course Calendar |

(c) 2001 Doug Davis; all rights reserved