Physics 1351

First Hour Exam

25 September1997

Possibly useful information:

s = s_i + v_i t + (¹/₂) a t²

v = v_i + a t

v² = v_i² + 2 a (s - s_i)

sin = ^opp/_hyp

cos = ^adj/_hyp

tan = ^opp /_adj

F = m a

F₁₂ = - F₂₁

f_smax = µ_s n

f_k = µ_k n

g = 9.8 m/s² = 10 m/s²

1. A hot air balloon is traveling vertically upward at a constant speed of 5.0 m/s. When it is 10.0 m above the ground, a sandbag is released from the baloon. (a) After it is released, for how long is the sandbag in the air? (b) What is its velocity just before impact with the ground!

(a) After it is released, for how long is the sandbag in the air?

y = y_i + v_i t + (¹/₂) a_y t²

y = y_i+ v_i t + (¹/₂) (- g) t²

0 = 10 m + (5 m/s) t + (¹/₂) (- 10 m/s²) t²

0 = 10 + 5 t + (¹/₂) (- 10) t²

0 = 10 + 5 t - 5 t²

5 t² - 5 t - 10 = 0

t² - t - 2 = 0

t = { - (-1) ± SQRT[ ( - 1)² - 4 (1) (-2)] }/2(1)

t = { 1 ± SQRT[ 1 + 8)] }/2(1)

t = { 1 ± SQRT[ 9] }/2

t = { 1 ± 3 }/2

t₁ = - 2/2 = - 1 = - 1 s (extaneous; throw out)

t₂ = + 4/2 = 2 = 2 s

t = 2 s

(b) What is its velocity just before impact with the ground!

v² = v_i² + 2 a (s - s_i)

v_y² = v_yi² + 2 a_y (y - y_i)

v_y² = (5 m/s)² + 2 ( - 10 m/s²) (0 - 10 m)

v_y² = 5² + 2 ( - 10) ( - 10 )

v_y² = 225

v_y = 15 m/s

v_y = 15 m/s

2. A ball is thrown from the floor of a canyon as shown in the sketch above. The ball is thrown with an initial speed of 30 m/s at an angle of 53° above the horizontal. It lands on the plateau above the canyon, 20 m above the canyon floor.

(a) How long is the ball in the air?

We need the y-component of the initial velocity,

v_yi = v_i sin = (30 m/s) sin 53^o = (30 m/s) (0.8) = 24 m/s

For what time do we find y = 20 m?

y = y_i + v_yi t + (¹/₂) a_y t²

y = 0 + (24 m/s) t + (0.5) ( - 10 m/s²) t²

Set y = 20 m and solve for the time t,

20 m = 0 + (24 m/s) t + (0.5) ( - 10 m/s²) t²

20 = 24 t - 5 t²

5 t² - 24 t + 20 = 0

t = [ - ( - 24) ± SQRT { ( - 24 )^2 - 4 (5) (20) }] / [ 2 (5) ]

t = [ 24 ± SQRT { 576 - 400 } ] / 10

t = [ 24 ± SQRT { 176 } ] / 10

t = [ 24 ± 13.3 ] / 10

t₁ = 37.3 / 10 = 3.73 sec

t₂ = 10.7 / 10 = 1.07 sec

t = 1.07 s

The time t₁ = 3.73 seconds is the time we want. At that time, the ball has gone up, reached its max height, and is on its way down as it strikes the plateau at y = 20 m. The time t₂ = 1.07 seconds is the time -- on its way up -- when the ball passes through y = 20 m.

 

(b) Where does it strike the plateau, 20 m above the canyon floor? That is, how far has it traveled horizontally when it strikes the plateau?

Now we are ready to ask how far the ball travels horizontally during that time of t = 3.73 s. For that, of course, we need the horizontal velocity,

v_x = v_xi = v_i cos = v_i cos 53_o = (30 m/s) (0.6) = 18 m/s

x = v_x t = (18 m/s) (3.73 s)

x = 67.1 m

3. Find the tension in the three ropes. Feel free to use the approximation of g = 10 m/s2.   Essentially by inspection, we can immediately set T3 = w = (10 kg) (10 m/s2) T3 = 100 N

Now we will concentrate on the "know" where the three ropes are joined. Since it is in equilibrium, the three forces must have a sum or resultant of zero.

F_net = F = T₁ + T₂ + T₃ = 0

F_net,x = F_x = T_1x + T_2x + T_3x = 0

T_1x + T_2x + T_3x = - T₁ cos 60^o + T₂+ 0 = 0

- T₁ (0.500) + T₂ = 0

0.500 T₁ = T₂

F_net,y = F_y = T_1y + T_2y + T_3y = 0

T_1y + T_2y + T_3y = T₁ sin 60^o + 0 - 100 N = 0

T₁ (0.866) = 100 N

T₁ = (100 / 0.866) N

T₁ = 115 N

T₂ = 0.500 T₁ = 0.500 (115 N)

T₂ = 57.5 N

T₃ = 100 N

---

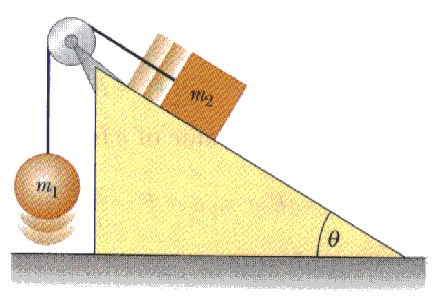
4. Consider the "inclined Atwoods machine" sketched above.

The masses are m₁ = 1 kg and m₂ = 3 kg.

The plane is inclined at an angle of = 37^o.

The coefficient of friction between mass m₂ and the plane is 0.1

Find the acceleration of the masses.

As always, start with good force diagrams:

We expect the acceleration to be upward and have that drawn beside the free-body diagram. As always, we are now ready to apply F = m a to these forces acting on this object. Fnet = F = T - m1 g = m1 a T - m1 g = m1 a T - (1 kg) (10 m/s2) = (1 kg) a As we might expect by now, this one equation has two unknowns -- tension T and acceleration a -- so we must look elsewhere for additional information. Of course, the place to look is at the other mass.

Carefully construct a free-body diagram showing all the forces acting on mass m₂.

There are four forces acting on this mass -- the string exerts a force T, the (frictionless) inclined plane exerts a "normal" force n, gravity pulls down with a force of w₁ = m₁ g, and there is the friction force F_f. To find the net force, we must resolve these vectors into their components. Since the acceleration will be along the direction of the plane, we have chosen that direction as the x-axis.

 Notice that the angle in this diagram is measured from the y-axis. That means the weight has components of

w_x = m₂ g sin = (3 kg)(10 m/s²) sin 37^o = (30 N) (0.6)

w_x = 18 N

w_y = - m₂ g cos = (3 kg)(10 m/s²) cos 37^o = (30 N) (0.8)

w_x = 24 N

And we have

n_x = 0

n_y = n

That is, the normal force has only a component in the positive y-direction.

F_f,x = - F_f

F_f,y = 0

That is, the friction force has only a component in the negative x-direction.

and

T_x = - T

T_y = 0

That is, the rope exerts only a component in the negative x-direction.

Now we can apply Newton's Second Law to this mass:

F = m a

F = F_net = T + n + w + F_f = m a

F_x = F_net,x = F_x = m₂ a_x

F_x = T_x + n _x + w _x + F_f,x = m₂ a_x

- T + 0 + 24 N - F_f = m₂ a_x = (3 kg) a

where we have used

a_x = a

since the acceleration is only in the positive x-direction.

- T + 24 N - F_f = (3 kg) a

But we do not yet know the friction force. We know only

F_f = n

F_f = 0.1 n

So we must find n, the normal force. We can do this by looking at the sum of the forces in the y-direction,

F_y = T_y + n _y + w _y + F_f,y = m₂ a_y = 0

T_y + n _y + w _y + F_f,y = 0

0 + n_y - 18 N + 0 = 0

n_y = 18 N

Therefore

F_f = (0.1) (18 N)

F_f = 1.8 N

Now,

- T + 24 N - F_f = (3 kg) a

becomes

- T + 24 N - 1.8 N = (3 kg) a

- T + 22.2 N = (3 kg) a

T = 22.2 N - (3 kg) a

Along with the equation from the hanging mass m₁, this provides all the information we need to solve for T and a. As before, we can solve one of these equations for T and substitute that into the other equation, from the hanging mass m₁, and solve for a.

T = 22.2 N - (3 kg) a

T - (1 kg) (10 m/s²) = (1 kg) a

[ 22.2 N - (3 kg) a ] - (1 kg) (10 m/s²) = (1 kg) a

22.2 N - (3 kg) a - 10 N = (1 kg) a

12.2 N = (4 kg) a

a = (12.2/4) (N/kg)

a = 3.05 m/s²

| Return to Course Calendar | Return to Dr D's Home Page |

(C) 1998, Doug Davis; all rights reserved