1350Ex1F01

PHY 1351
General Physics I

First Hour Exam
September 21, 2001

Statistics:

High: 80

Mean: 46

Low: 18

You simply cannot survive this course without doing the homework. This is a homework-intensive, labor-intensive, time-intensive course. it is not difficult, per se. But it does require time!

Possibly useful information:

v = v_i + a t
x = x_i + v_i t + (¹/₂) a t²
v² = v_i² + 2 a x
a_c = v²/r
F = m a
F₁₂ = – F₂₁
sin = ^opp/_hyp
cos = ^adj/_hyp
sin = ^opp/_adj

Conceptual Questions:
Besides a “yes” or “no”, be sure to explain your answers.

C1: If the velocity of a particle is nonzero, can its acceleration be zero?

YES. Acceleration is the change in the velocity divided by the change in time. So if the velocity is nonzero, it could readily be changing (or not changing!). A particle with nonzero velocity could have any kind of an acceleration.

C2: The magnitudes of two vectors A and B are A = 5 units and B = 2 units. What are the largest and smallest values possible for the resultant vector R = A + B ?

When vectors A and B point in the same direction, their resultant R will have a magnitude of (5 + 2 = ) 7 units; this is maximum.

When vectors A and B point in the opposite direction, their resultant R will have a magnitude of (5 - 2 = ) 3 units; this is minimum.

C3: Can an object accelerate if its velocity is constant?

NO. Acceleration is the change in the velocity divided by the change in time. So if the velocity is constant, it is not changing which means the acceleration is zero.

C4: What forces cause a propeller-driven airplane to move?

As the propeller pushes on the air, the air pushes back on the propeller. This force of the air on the propeller cause the propeller -- and the airplane -- to move. This is an example of the action-reaction force pairs of Newton's Third Law.

P1: A car brakes from 100 ^km/_h to rest in a distance of 75 m.

a) What was the initial speed in units of ^m/_s?
v_i = 100 ^km/_h [^{1 000 m}/_km] [^h/_{3 600 s}] = 27.8 ^m/_s

b) What is the acceleration of the car?
v² = v_i² + 2 a x
0 = (27.8 m/s)² + 2 a (75 m)
2 a (75 m) = - (27.8 m/s)²
a = - (27.8 m/s)²/150 m
a = - 5.14 m/s²

c) How much time does the car require to stop?
v = v_i + a t
0 = 27.8 ^m/_s + ( - 5.14 m/s²) t
t = [27.8 m/s]/[5.14 m/s²]
t = 5.41 s

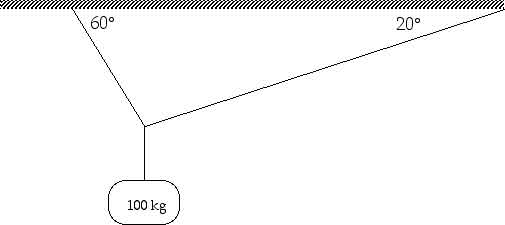
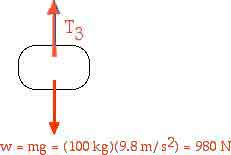
P2: A 100-kg mass hangs from ropes suspended as shown in the diagram below. Find the tension in each of the ropes.

Almost by intuition we can easily find that

T₃ = mg = 980 N

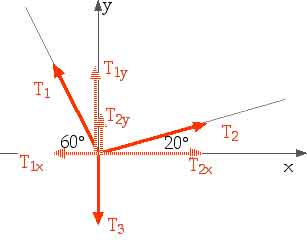
Now we turn our attention to the "knot" where the three ropes meet. That is not moving so we know F_net = 0

F_net = T₁ + T₂ + T₃ = 0

Remember(!) this is a vector equation; this really means

F_net,x = T_1x + T_2x + T_3x = 0	F_net,y = T_1y + T_2y + T_3y = 0
- T₁ cos 60^o + T₂ cos 20^o + 0 = 0 - T₁ (0.500) + T₂ (0.940) + 0 = 0 0.50 T₁= 0.94 T₂ T₁= 0.94 T₂/0.50 T₁= 1.88 T2 T₁= 1.88 (497 N) T₁ = 935 N	T₁ sin 60^o + T₂ sin 20^o - T3 = 0 T₁ (0.866) + T₂ (0.342) - 980 N = 0 0.866 T₁ + 0.342 T₂ = 980 N 0.866 (1.88 T₂) + 0.342 T₂ = 980 N 1.97 T₂ = 980 N T₂ = 497 N

P3: A football is kicked at an angle of 60° above the horizontal with an initial speed of 20 m/s. The ball is kicked from the base of an inclined plane that is inclined 20° above the horizontal.

Where does the ball land on the inclined plane? That is, how far from the base of the inclined plane does the ball land?

v_ix = (20 ^m/_s) cos 60^o = (0.500)(20^m/_s) = 10.0 ^m/_s

v_iy = (20 ^m/_s) sin 60^o = (0.866)(20 ^m/_s) = 17.32 ^m/_s

The trajectory of the football is given by

x = x_i + v_ix t + (¹/₂) a_x t²

y = y_i + v_iy t + (¹/₂) a_y t²

where

a_x = 0

a_y = - g

and

y_i = 0

x_i = 0

which then means

x = 0 + v_ix t + 0

x = (10.0 ^m/_s) t

y = 0 + v_iy t - (¹/₂) g t²

y = (17.32 ^m/_s) t - (¹/₂) (9.8 m/s²) t²

These are "parametric equations" in the parameter t. For an equation in only x and t, we can solve for t from the x-equation (because it is a simpler, linear equation),

t = x/(10 ^m/_s)

and then substitute that into the y-equation,

y = (17.32 ^m/_s) [x/(10 ^m/_s)] - (¹/₂) (9.8 m/s²) [x/(10 ^m/_s)]²

y = 1.732 x - 0.049 x²

Remember, this is the equation of the trajectory, the path the football follows.

(I have not been entirely careful with the units. x and y are measured in meters(m) so x² has units of m². I have chosen not to carry that through; so this equation now requires that x and y be measured in m).

The inclined plane can be described by the equation

y = x tan 20^o = 0.364 x

y = 0.364 x

Where do these two "curves" or lines intersect? We can set the two equations for y equal to each other,

y = 0.364 x = 1.732 x - 0.049 x² = y

0.364 x = 1.732 x - 0.049 x²

0.049 x² - 1.368 x = 0

(x)(0.049 x - 1.368) = 0

x = 0

True, but not very interesting, . . . or

0.049 x - 1.368 = 0

0.049 x = 1.368

x = 1.368/0.049

x = 27.92 m

y = 0.364 x = 0.364 (27.92 m)

y = 10.16 m

R = SQRT[x² + y²] = SQRT[(27.92)² + (10.16)²] m

R = 29.71 m

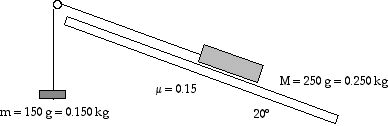
P4: A 150 g mass is suspended as shown in the diagram. It is attached to a string which runs over a pulley and is then attached to a 250-g block which slides along an inclined plane as shown in the diagram.
The inclined plane is inclined at 20° with the horizontal. The coefficient of friction between the block and the plane is 0.15. (this was corrected on the board in class).
Find the acceleration of the masses and the tension in the string.

Always(!) begin with good, clear "free body diagrams" showing all the forces on each of the masses.

I am expecting this block to come down - so I have written the acceleratio pointing down and have taken down as positive:

F = m a

F_net = m a

F_{= w - T = m a}

1.47 N - T = (0.150 kg) a

I am expecting this block to accelerate in the direction shown - so I have taken the positive x-direction as shown, up and to the left.

As we discussed in class, there are other ways to do this. There is seldom (if ever!) only a single "right way" to solve a Physics problem.

F = m a
F_net,x = m a T - F_fr - 0.838 N = (0.250 kg) a F_fr = (0.15)(2.302 N) = 0.345 N T - 0.345 N - 0.838 N = (0.250 kg) a T - 1.183 N = (0.250 kg) a	F_net,y = m a_y n - 2.302 N = m (0) n = 2.302 N

We now have two equations with two unknowns, the tension T and the acceleration a,

T - 1.183 N = (0.250 kg) a

1.47 N - T = (0.150 kg) a

Solve for T from the first one,

T = 1.183 N + (0.250 kg) a

and subsitute that into the second one for T,

1.47 N - [1.183 N + (0.250 kg) a] = (0.150 kg) a

1.47 N - 1.183 N = (0.150 kg) a + (0.250 kg) a

0.29 N = (0.400 kg) a

(0.400 kg) a = 0.29 N

a = 0.725 m/s²

Now we can use this acceleration to find the tension T,

T = 1.183 N + (0.250 kg) a

T = 1.183 N + (0.250 kg) (0.725 m/s²)

T = (1.183 + 0.181) N

T = 1.364 N

Return to PHY 1350's Home Page