
Vertical Spring and Hanging Mass
Our prototype for SHM has been a horizontal spring attached to a mass,
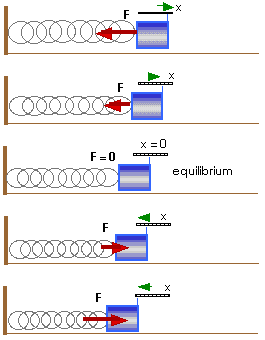
But it is often easier for us to set up a vertical spring with a hanging mass. Now the force of gravity comes into play. Does this change what we expect for the period of this simple harmonic oscillator?
Consider a vertical spring on which we
hang a mass m; it will stretch a distance ![]() x
because of the weight of the mass,
x
because of the weight of the mass,
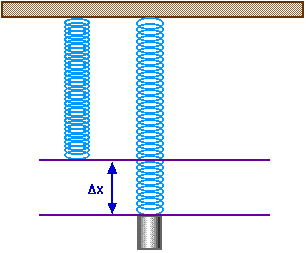
That stretch is given by ![]() x
= m g / k. k is the spring constant of the spring.
x
= m g / k. k is the spring constant of the spring.
Now pull the mass down an additional distance x',

The spring is now exerting a force of
Fspring = - k (x' + ![]() x)
x)
Fspring = - k x' - k
![]() x
x
Fspring = - k x' - mg
When we add in the force of gravity, we have
Fnet = - k x' - mg + mg
Fnet = - k x'
Now this looks exactly like our prototypical equation with the displacement x' now being measured from the new equilibrium position. This means that everything we have learned about our prototypical horizontal SHO is entirely applicable to this more usual vertical SHO.
|
|
|
|
|
|
|
|
||
|
|
|||