Simple Pendulum

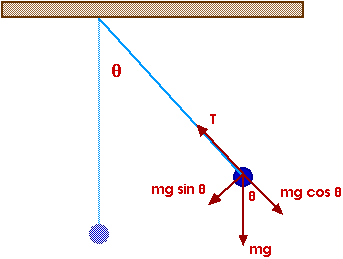
The net restoring force is

F_net = - m g sin

- m g sin = m a

a = - g sin

And this is not exactly what we had for our prototype,

F_net = - k x = ma

a = - ( k / m ) x

Or is it?

Look more closely at this sin :

sin = opp / hyp

sin = opp / hyp

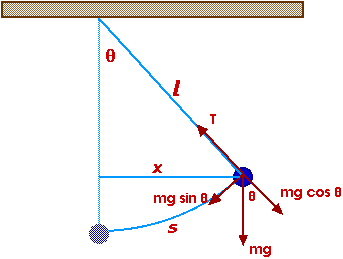
sin = x / l

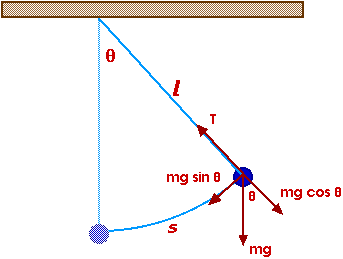
And for small angles, this is nearly equal to

sin = s / l

Now we have

a = - g sin

or

a = - g (s / l)

or

a = - ( g / l ) s

where s is the displacement from equilibrium.

So this simple pendulum is a SHO for small angular displacements!

It is interesting and useful to look at the sine function as a power series expansion

sin x = x - (x³/3!) + (x⁵/5!) - (x⁷/7!) + . . .

That means, for small angles x,

sin x = x

and sin x deviates from that like x³ so we must go to very large angles x to see a difference from sin x = x. If we watch a simple pendulum with very large amplitude we find that it is not a simple harmonic oscillator (SHO). But it is a very close approximation for small amplitudes!

Vertical Spring			Torsional Pendulum
Return to ToC, Simple Harmonic Motion

(c) Doug Davis, 2001; all rights reserved