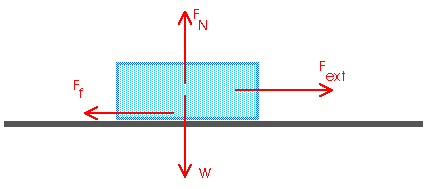
Static Friction
The force of friction always opposes the motion -- or opposes the motion that would occur if the friction force were not present.
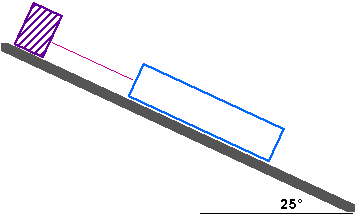
Example: The weight is 100 newtons; what is the tension in the
cord supporting it? The coefficent of friction between the block
and the plane is 0.35.
Always start with a free body diagram showing all the forces acting on the body.
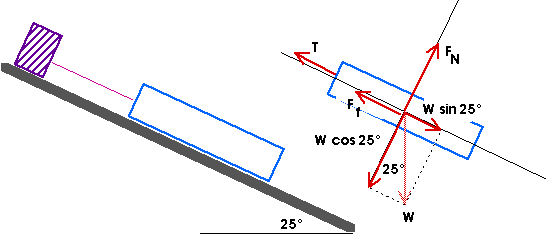
The x- and y-axes have been chosen parallel and perpendicular to the plane. From that diagram, we find the components of the weight are
Wy = - W cos 25° = - 90.6 N
The normal force FN lies in
the positive y-direction; the tension T and friction force
Ff lie along the negative x-axis. Notice that the
friction force is its maximum value 
FN
if the rope is required to hold the block in equilibrium. Now we
have all the components required for the First Condition of
Equilibrium.
The First Condition of Equilibrium, for the x-components of all the forces, is
Fx
= W x - Ff - T = 0
Wx - Ff,max - T = 0
Wx - FN
- T = 0
42.3 N - 0.35 FN - T = 0
The First Condition of Equilibrium, for the y-components of all the forces, is
Fy
= F N - W y = 0
FN - 90.6 N = 0
FN = 90.6 newtons
This value of the normal force can be substituted
back in the Fx
equation to find
T = 10.6 newtons
If we wanted to know the friction force, we would find that from
FN
= (0.35)(90.6 N) = 31.7 N
Notice that the normal force FN is not equal to the weight in this case.
There are just enough special cases where the normal force does happen to be equal to the weight that it is sometimes (and wrongly) assumed that the normal force and weight are always the same. Be aware of that for it simply is not true!
 |
 |
|
 |
|
|
|
||
|
|
|||