Elastic Properties of Solids
Cause ==>
Effect
Cause ==>
Deformation
"Force" ==>
Deformation
What kinds of deformations will we encounter?
Length deformationCompressionTensile / stretch
Shear
Bulk compression
Length deformation as an example
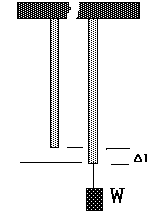
But how can we describe the material itself--independent of the geometry?
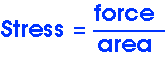
Stress is "cause".
Stress is measured in newtons per square meters; this is known as a pascal, Pa.
1 pascal = 1 Pa = 1 [ N /
m2 ]
Strain is "effect" or "result".
A modulus describes a material's behavior with regard to stress and strain. How easily is it deformed?
Length deformation
What does all this mean for length deformation -- stretching or compressing?
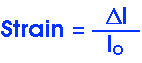
The "length deformation modulus" is known as Young's Modulus,
Young's Modulus is the slope of the line for the elastic region of this Stress / Strain graph.
Click here
for an EXAMPLE.
Shear Modulus
Bulk Modulus
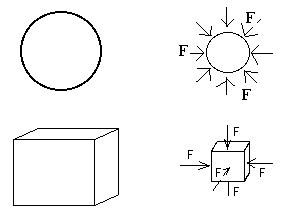
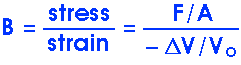
But F/A is just the pressure which we will talk about later. Therefore, we can also write the definition of the Bulk Modulus as
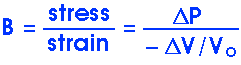
Notice the minus sign. This is necessary because an increase in pressure causes a decrease in volume.
|
 |
|
|
|
|
|
||
|
|
|||