Newton's Second Law

for Rotation about a Fixed Axis

Just because it moves in a circle, an object of mass m must have a centeral force on it -- a radial force, a force toward the center, or a centripetal force.

In addition, consider an object of mass m that has a tangential force on it F_t,

This means the mass m will have a tangential acceleration, a_t

F_t = m a_t

For a moment, think of this as a mass m embedded in a massless disk -- like a thin sheet of plexiglass or a thin piece of aluminum. How can we relate this tangential accleration of the small mass m to the angular accelration of the entire "system" or disk?

We know

a_t = r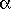

The torque due to a tangential force is clearly

= r F_t

= r ( m a_t )

= r m ( r )

= [ m r ² ]

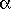
= I

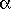
where, again,

I = m r²

is the moment of intertia, the rotational equivalent of the mass, indeed, the "rotational mass".

Notice, of course, that this rotational version of Newton's Second Law,

= I

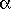
looks very much like the linear form

F = m a

with which we are already quite familiar.

This immediate example had only a single mass m. If more masses are involved then, just as before, the moment of inertia is

I = [ m_i r_i²]

and, for an extended or continuous object, this becomes

r is still the perpendicular distance from the axis of rotation.

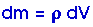
Typically the density will be a constant so we will have

 

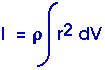
Once the moment of inertia is found or given, we are back to applying Newton's Second Law -- this time for rotation,

= I

	Examples
Torque			Work, Power, and Energy
Return to ToC, Ch10, Rotation about a Fixed Axis

(c) Doug Davis, 2001; all rights reserved