Center of Mass - Example
The Center of Mass is the average position of the mass of an object. It is a uniquely interesting point. We may consider an object as a hollow, massless shell with all its mass located at this Center of Mass (CoM). For a continuous distribution of mass, the coordinates of the CoM are given by
and
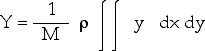
where
The textbook calculates the CoM for a rod and of a right triangle on page273. Be sure that you understand those examples.
Your textbook already does the most interesting and most important examples
that use Cartesian coordinates (x and y). We will look at polar coordinates
(r and 
).
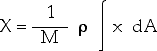
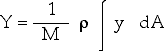
Now we must ask what this small, differential area dA is
in polar coordinates. Any point can be designated with cartesian coordinates
(x, y) or with polar coordinates (r, ).
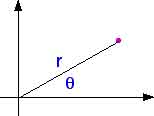
If each of the coordinates increases a differential amount (dr
and d) the area that is
created is the differential area dA.
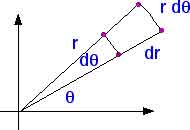
dr is easy. d,
however, may require a little thought. The length that it traces out
depends upon the value of the radius r. The differential area dA is (dr) multiplied
by (r d):
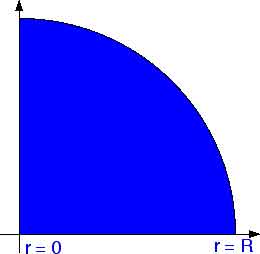
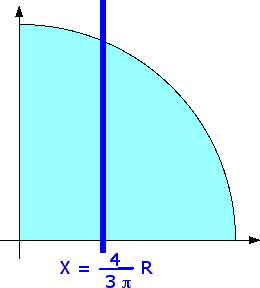
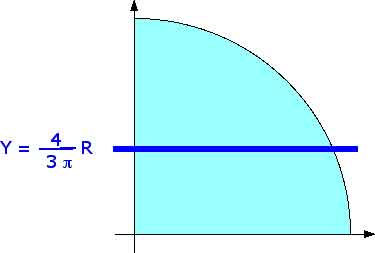
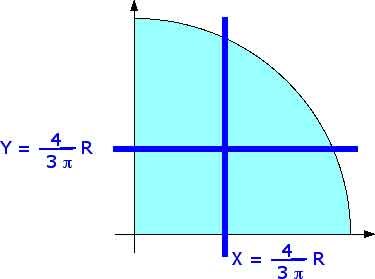
We are going to apply this to finding the center of mass of a quadrant of a circle (of radius R).
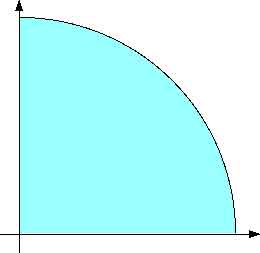
Here is our representative differential area dA,
We will first carry out an integral over
from = 0 to
= 90o.
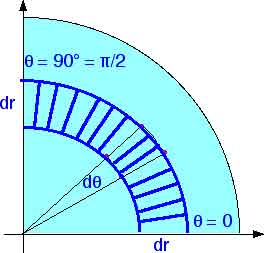
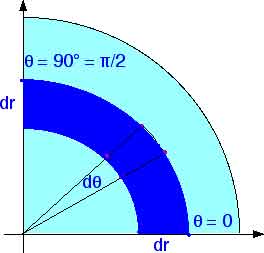
That will give us a representative band or strip of thickness dr.
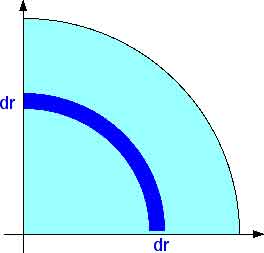
We will then integrate over r from r = 0 to r = R.
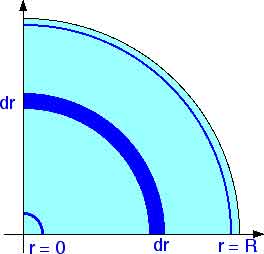
That will take care of the entire area of the quadrant of the circle.
We have equations
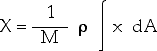
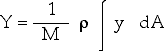
for the center of mass. By symmetry, however, we know that X = Y so when we
solve for one of them we have solved for both of them. Toss a coin and let's
get started. We might as well start with the x-coordinate. How do we get x (or
y) from r and ?
x = r cos
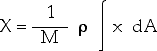
becomes
|
 |
|
|
|
|
|
||
|
|
|||
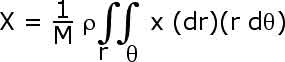
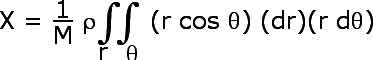
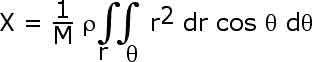
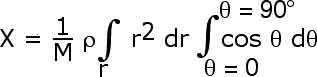
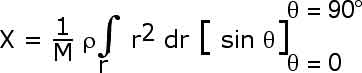
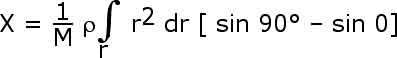
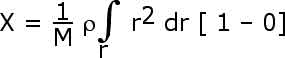
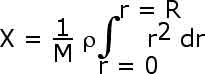
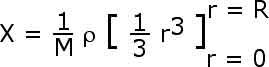
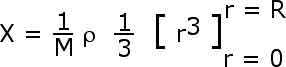
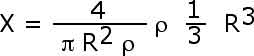
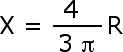
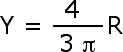