Conservation of Momentum

Center of Mass

The Center of Mass is the average position of the mass of an object. It is a uniquely interesting point. We may consider an object as a hollow, massless shell with all its mass located at this Center of Mass (CoM).

When we throw a baseball, we expect it to follow a smooth, parabolic trajectory as we have discussed with projectile motion.

When we throw a baseball bat, however, its path or trajectory does not seem smooth at all. While the bat rotates around the center of mass, the center of mass itself is following the same smooth, parabolic path that we expect for a smaller, simpler object, like a baseball.

The center of mass itself follows the same smooth path that we expect for a smaller, simpler object, like a "point particle".

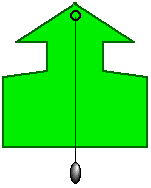
How can we locate the Center of Mass in an extended object?

We can suspend it. The Center of Mass will always be directly under the point of support.

Then we can suspend it from some other point and know that the Center of Mass will always be directly under this point of support as well.

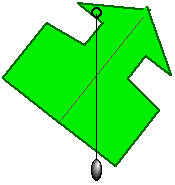
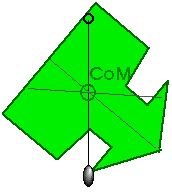
Remember that we can think of any object as a rigid, massless shell with all its mass concentrated at the Center of Mass.

How does this effect the stability of an object?

If an object moves a little, what happens to its Center of Mass? Does it move up? Does it move down?

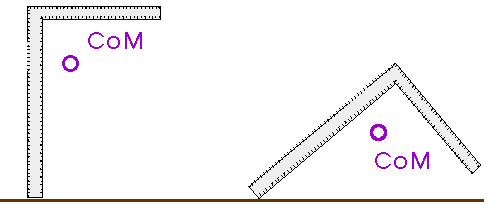
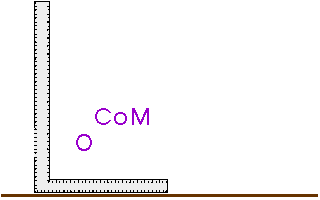
If a small movement lowers the CoM, the object is unstable.

If a small movement raises the CoM, the object is in stable equilibrium.

What is the difference between Center of Mass and Center of Gravity?

The two terms are often used almost interchangeable -- just as mass and weight are closely connected.

When we talk of astronomical objects -- certainly galaxies, but even our own Earth and moon -- there is a difference.

Now that we know the Center of Mass as the average position of the mass, what can we do with it or how can we calculate a value for it?

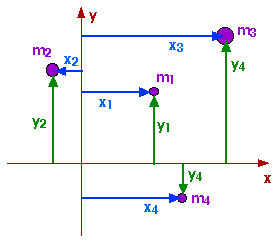
Consider a "collection" of individual masses, m_i, located on a rigid, massless sheet --

We can locate each of these with a vector, r_i, and write the "average position" or the position of the Center of Mass, R, as

R = r_i m_i / m_i

Before you go on, think of how you might find the average grade in this class or the average height of people in this class -- or the average anything. This definition of the location of the Center of Mass is just the mass-weighted average of the position.

Numerical Examples

While it is nice and elegant to write this as a vector equation,

R =

r_i m_i /

m_i,

calculations almost always demand the corresponding scalar equations. That is, we can define the separate coordinates of the Center of Mass, X, Y, and Z (altho' we will usually stay with two-dimensional systems and only need X and Y) as

X =

x_i m_i /

m_i

Y = y_i m_i / m_i

and, just to be "complete",

Z = z_i m_i / m_i

This is also an excellent opportunity to extend this idea to a continuous mass distribution and replace these summations with integrals. For this, however, we will limit our present discussion to two dimensions.

For discrete masses, we have

X = x_i m_i / m_i

Y = y_i m_i / m_i

We begin by replacing the individual, discrete, separate masses m_i with a "representative" mass dm,

dm =

dA =

dx dy

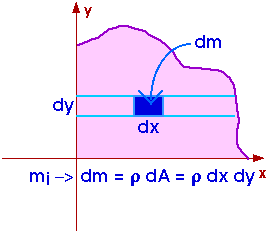
is the surface mass density with units like grams per square centimeter ( g/cm² ).
The summations are replaced by integrals -- the limits are (very) important. That is,

X = x_i m_i / m_i

becomes

and

Y = y_i m_i / m_i

becomes

where M is the total mass. For individual, discrete masses we could write

Now, for a continuous distribution of mass, the total mass M is found by

The limits and the details of how to actually evaluate these integrals are very important!

We can begin by summing the little dm's from x = 0 to x = Edge where Edge = Edge(y) is the edge of the boundary and will almost surely depend upon y. Particular examples will help provide understanding.

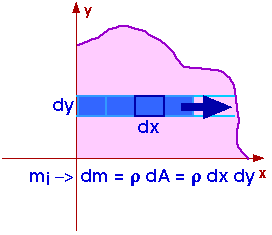
When this integral over x is completed, we have a "representative" strip of thickness dy and we can sum it over y from y = 0 to y = TOP where TOP is the maximum value of y at the boundary.

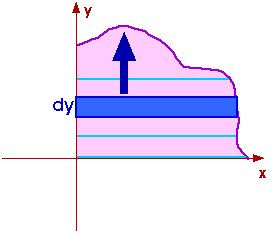
Look at particular examples from Serway's text and from your notes of our discussion in class.

| CoM Examples |

2D Collisions

Rocket Propulsion

Return to ToC, Ch9, Linear Momentum


2D Collisions			Rocket Propulsion
Return to ToC, Ch9, Linear Momentum