Potential Energy

Gravity provides a nice example of work done by a force that can be considered Potential Energy. Potential Energy is sometimes written as PE or V. Most common is the notation of the text where Potential Energy is written as U. How much work does the force of gravity do on an object of mass m as the mass moves from initial height y_i to final height y_f?

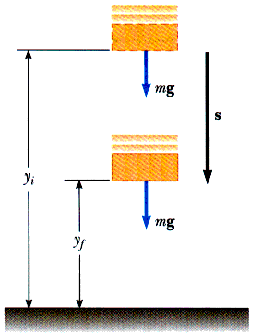
W_g = (F_g) s = (m g) s = ( - m g j) ( y_f - y_i ) j = - m g y_f + m g y_i

We could even get carried away with this and write a more general form of the displacement s,

Let s = ( x_f - x_i ) i + ( y_f - y_i ) j

Then the work done by gravity is

W_g = (m g) s = ( - m g j) [( x_f - x_i ) i + ( y_f - y_i ) j ] = - m g y_f + m g y_i

The horizontal component of the displacement does not make and difference!

In either case, we have

W_g = - m g y_f + m g y_i

This means we can define the gravitational potential energy as

U_g = m g y

and then we can write the work done by the force of gravity as

W_g = - ( U_f - U_i )

Notice the order of these subscripts,

W_g = - U = - (U_f - U_i)

U -- the change in potential energy -- is the final value minus the initial value.

W_g = - U

ToC			Conservative Forces
Return to ToC, Ch8, Conservation of Energy

(c) Doug Davis, 2001; all rights reserved