Work Done by a Varying Force

How do we "handle" a force that is not constant? That is, how much work is done by a varying force? We know how to find the work done by a constant force,

W = F s cos

How much work is done by a varying force such as this one?

Since we do know how to handle a constant force, we can break this one up into "average values" over small distance x, like this,

Each of these little rectangles has an "area" of (F_x)(x); this is an amount of work W. That is

W = F_x x

for each of these little rectangles. The total amount of work done is the sum of these rectangles,

W_Tot = W = 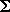W

W = F_x x

In the limit, as we make x smaller and smaller, this sum becomes an integral,

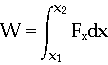
Scalar Product			Kinetic Energy
Return to ToC, Ch7, Work and Energy

(c) Doug Davis, 2001; all rights reserved