Relative Motion

Galilean Relativity

Consider two observers, A and B, moving relative to each other. How can we compare their observations?

In particular, consider two reference frames, labeled A and B, which move relative to each other with constant velocity v, oriented so they are parallel and their x-axes align with their relative velocity. The velocity of frame B relative to A is v and the velocity of frame A relative to B is &endash; v. Further, to simplify matters, we start our clocks or stopwatches when the origins of the two reference frames coincide. All this is shown schematically below.

Now consider an object located at point P. Observers in both frames record its position and velocity. Of course, they get different numbers but these numbers can be related to each other by using these transformation equations:

x_A = x_B + vt

y_A = y_B

v_Ax = v_Bx + v

v_Ay = v_By

where x_A and y_A are the coordinates of point P measured by observer A while x_B and y_B are the coordinates measured by observer B; v_Ax, and v_Ay are the components of P's velocity measured by A, and v_Bx and v_By are the velocity components measured by B. Everybody measures t for the time and v is the relative speed of the two observers. These equations are the Galilean Relativity Transformations. The position equations may be combined and written in vector form as

r_A = r_B + v t

while the velocity equations may be combined and written in vector form as

v_A = v_B + v

All these transformation equations may be seen in the following schematic diagram:

We expect Newton's First Law, the Law of Inertia, to be valid for both observers. We expect both these frames to be inertial frames. If Newton's Law of Inertia is valid, all the other laws of Mechanics--and ideas like conservation of energy, conservation of momentum, and conservation of angular momentum--will also be valid.

The relative motion need not be along one of the axes, of course. Consider a point P that is located by displacement vector r_p1 with respect to reference frame 1 and located by displacement vector r_p2 with respect to reference frame 2. And reference frame 2 is located by vector r₂₁. This is shown here, in this sketch,

These displacement vectors are related by

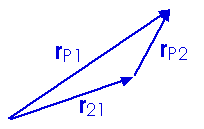
Notice the details of the subscripts,

We can then take the time derivative of this equation to find the speed of point P as seen by the two reference frames,

This equation corresponds to the diagram and assumes that we know the velocity v_p2 in reference frame 2 and the relative velocity v₂₁. If, instead, we know the velocity v_p1 in reference frame 1 and the relative velocity v₂₁, we can simply solve for v_p2,

If the two reference frames move with constant relative velocity, then taking the time derivative one more time provides

That is, the acceleration seen by observers in the two reference frames is the same.

---

Example

A boat heads due North across a river with a speed of v_br = 10 km/h relative to the water. The river has a speed of v_rE = 5 km/h due East, relative to Earth. Determine the velocity of the boat relative to Earth v_bE (that is, the velocity of the boat relative to an observer watching from the bank of the river).

We can write the appropriate relative velocity equation,

v_bE = v_br + v_rE

v_bE = SQRT [ v_br² + v_rE² ]

v_bE = SQRT [ ( 10 )² + ( 5 )² ] km / h

v_bE = 11.2 km / h

= tan^-1 (^opp/_adj) = tan^-1 ( 5 / 10 ) = tan^-1 (0.50) = 26.6^o

---

Example

Now we want to cross the same river with the same boat. But, this time, we want to go directly across the river. At what angle, upstream, must we head so that our velocity relative to Earth, v_bE, is directly across the river. What is our new speed v_bE, relative to Earth (or our land lubber observer sitting on the bank)? Our vector equation is still

v_bE = v_br + v_rE

but our vector diagram looks quite different now,

The magnitude (or lenght) of vector v_br is still 10 km/hr.

v_br² = v_bE² + v_rE²

v_rE² = v_br² - v_bE²

v_rE² = [ ( 10 )² - ( 5 )² ] km/hr

v_rE = SQRT [ ( 10 )² - ( 5 )² ] km/hr

v_rE = 8.66 km / hr

= tan^-1 (^opp/_adj) = tan^-1 ( 5 / 8.660 ) = tan^-1 ( 0.577 ) = 30^o

---

Return, for a moment, to our two observers A and B.

Observers A and B "see" different things. But both agree that the Laws of Physics are the same.

What do they observe for the speed of light?

Experimentally, both observers find the same value for the speed of light !

How can this be? Stay tuned . . . until we reach Modern Physics and Special Relativity. Many interesting and unexpected things wait for us along the journey.

Acceleration			Relative Motion at High Speeds
Return to ToC, Ch4, Two-Dimensional Motion

(c) Doug Davis, 2001; all rights reserved