Projectile Motion

Projectile motion is motion under the influence of gravity. If we stand at the edge of the roof of the Science Building and throw a ball up at an angle, it moves up and then down vertically while it moves horizontally.

This is projectile motion.

To better understand this projectile motion, let's move back and then look at it through the eyes of two different and special observers.

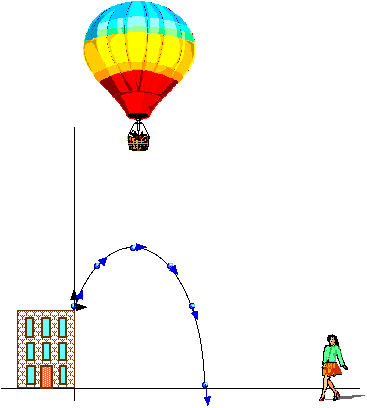
What is the motion seen by a far-distant observer on the ground?

This observer is far enough away she has lost depth perception but can clearly see the ball rise and fall. She observes free fall, just as if the ball were thrown straight up. This is vertical motion with constant acceleration.

What motion is seen by an observer overhead? This overhead observer is high enough that he has lost depth perception but can clearly see the ball move horizontally. He observes horizontal motion with constant velocity.

Projectile motion, then, is a combination of vertical motion with constant acceleration (free fall that we have already discussed) and horizontal motion with constant velocity (which we also understand).

---

Example

To make the arithmetic easy, let's use the approximation that g = 10 m/s² and throw a ball from the top of the Science Building and look at its velocity and position.

We throw the ball so it moves up with an initial vertical velocity of v_yo = 20 m/s and so it moves horizontally with an initial horizontal velocity of v_xo = 15 m/s.

We could also describe this as having an initial velocity of v_o = 25 m/s at an angle of 53° from the horizontal. For angles measured from the horizonta, we know

v_xo = v_o cos

v_yo = v_o sin

Look at the horizontal components; look at the v_x's. This is horizontal motion with constant velocity.

Look at the vertical components; look at the v_y's. This is common, ordinary free fall; this is vertical velocity with constant acceleration.

Now we will throw the ball yet another time. This time we will look at its position or its displacement.

These displacements come from the x- and y-component equations,

x = x_o + v_xo t + ¹/₂ a_x t²

and

y = y_o + v_yo t + ¹/₂ a_y t²

---

Parabolic Trajectories

Water -- from a water fountain or a garden hose or a fire hose -- offers an example of projectile motion that is easy to see. The shape of this path of water is a parabola.
When a ball is in motion -- after being spiked or hit or thrown or kicked or dunked -- it undergoes projectile motion and follows the path of a parabola.

---

Another Example

---

More Examples

It is fun and interesting to look at things like the Maximum Height or the Maximum Distance, called the Horizontal Range. But, please, treat these as interesting examples to be solved or derived rather than important formulas to be memorized.

From a level surface, how far will a projectile go?

We begin by firing a projectile with initial velocity v_o, that is with initial speed v_o at angle . It starts from the origin, (x_o = 0, y_o = 0). How far does it move horizontally before it is back at its original vertical position (y = 0) again.

While it may be more convenient or more common to describe the initial velocity v_o in terms of its speed v_o and angle , it is easier -- and necessary -- to solve the equations in terms of the x- and y-components of the initial velocity.

v_xo = v_o cos

v_yo = v_o sin

To find out how far it goes, we must first find out how long it is in the air. One way is to look at how long it takes to get to the top. At the top, the vertical component, the y-component, of the velocity is zero. We could find the time it takes for v_y to vanish. It will require twice this time to come up and back down to the ground.

Perhaps a more direct approach is just to find the time required to get back to the ground, to get back to y = 0. We know the vertical motion is explained by

y = y_o + v_yo t + ¹/₂ a_y t²

where the acceleration is

a_y = - g

and

v_yo = v_o sin

and

y_o = 0

Therefore

y = 0 + (v_o sin ) t - ¹/₂ g t²

We will set this equal to zery, y = 0, and solve for the time t,

(v_o sin ) t - ¹/₂ g t² = 0

(v_o sin ) t - ¹/₂ g t ) t = 0

There are two solutions,

t = 0

and

t _tot = t = (2 v_o sin ) / g

Both these times are "true". The first, t = 0, refers to the initial time when the projectile left y = 0. The second, t_tot, refers to the time when the projectile gets back to y = 0; that is the one of interest.

How far, horizontally, has the projectile moved in this time?

x = v_x t

Range = X_max = x(t_tot) = v_xo t_tot = (v_o cos ) (2 v_o sin ) / g

X_max = 2 v_o² cos sin / g

Since this expression contains

cos sin

and

cos = sin (90^o - )

this means that the range is the same for an angle and for its complimentary angle (90^o -). That is, for the same initial speed v_o, initial angles of 30^o and 60^o provide the same range. Initial angles of 20^o and 70^o provide the same range.

We can play a bit with trig identities and recall that

2 cos sin = sin 2

to rewrite the range equation as

X_max = v_o² sin 2 / g

From this form of the range equation, we can also see that the maximum value of the range occurs for

= 45^o

since the maximum value of sin 2 is 1.0 when 2 is 90^o, or = 45^o.

---

Another Example

Projectile motion does not need to begin and end on a horizontal plane. We have already thrown a ball from the top of the Science Building and watched it hit the ground 25 m below. Now, let's throw a rock from the bottom of a cliff and ask where it lands on the ground above.

A rock is thrown with an initial speed of 30 m/s at an angle of 60^o above the horizontal. As shown in the sketch, it is thrown from a canyon floor and goes up into the air and then lands on the plateau, 20 m above the canyon floor. Where does it hit the ground? Or, how far does it travel horizontally?

Perhaps the very first thing to do is to restate the initial velocity in terms of its components; we know

v_xo = v_o cos

v_xo = (30 m/s) (0.50)

v_xo = 15 m/s

and

v_yo = v_o sin

v_yo = (30 m/s) (0.866)

v_yo = 26 m/s

Before we can answer "how far" it travels, it is easier to ask "how long" is it in the air? We know its y-position is given by

y = y_o + v_yo t + ¹/₂ a_y t²

We need the time for which the y-coordinate is at the plateau, y = 20 m.

20 m = 0 + (26 m/s) t + ¹/₂( - g ) t²

20 m = (26 m/s) t + ¹/₂( - 9.8 m/s² ) t²

20 m = (26 m/s) t - ( 4.9 m/s² ) t²

20 = 26 t - 4.9 t²

4.9 t² - 26 t + 20 = 0

Solve this from the quadratic equation,

t₁ = 0.9 s

t₂ = 4.4 s

What is the meaning of these two times? t₁ is the time the rock passes the level of the plateau on its way up. t₂ is the time the rock is at the plateau on its way down; t₂ is when it lands on the plateau. That is the time we want. How far has it traveled horizontally during this time?

X_max = v_xo t₂

X_max = (15 m/s) (4.4 s)

X_max = 66 m

2-D Motion			Circular Motion
Return to ToC, Ch4, Two-Dimensional Motion

(c) Doug Davis, 2001; all rights reserved