Vector Components

We can describe any vector V in terms of its magnitude V and its direction . Here, we are measuring angle from the positive x-axis. And angle is positive for counter clockwise directions. Other coordinate systems may also be used; it is also common to measure angles from North.

We can also describe a vector V in terms of its components along the x- and y-axes,

V = V_x + V_y

How are these two descriptions related?

How are these two descriptions related? We have already seen that

V_x = V cos

V_y = V sin

for this coordinate system. We will use those relationships shortly.

Now consider a second vector U. It, too, may be expressed in terms of its components,

U = U_x + U_y

How can we add vectors U and V in terms of their components? That is, we want a resultant vector R that is

R = U + V

R = (U_x + U_y) + (V_x + V_y)

Since U = U_x + U_y and V = V_x + V_y, we may eliminate the vectors U and V from our diagram.

Now let us continue with our vector addition. Add the x-components together by themselves and then add the y-components together by themselves.

R = (U_x + V_x ) + ( U_y + V_y)

R_x = U_x + V_x

and

R_y = U_y + V_y

But look at these diagrams. While we have written R_x = U_x + V_x and R_y = U_y + V_y as vector addition equations, they are rather unusual vector equations. All the x-componets lie along the x-axis and all the y-components lie along they y-axis. So these particular equations are also true as scalar addition equations!

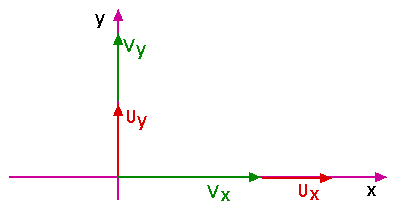
That is,

R_x = U_x + V_x

and

R_y = U_y + V_y

Finding the components of the resultant, then, has been reduced tor ordinary, commonplace, scalar addition!

Now that we know the components of the resultant, we can use them to reconstruct the resultant itself.

This will involve trig functions and the Pythagorean theorem.

Now that we have the idea, let's apply this numerical method of vector addition to the vector addition problem of the treasure map:

Vector A has only an x-component, so we can write

A_x = 5 paces

A_y = 0

"Northeast" means = 45^o, so

B_x = (7 paces) (cos 45^o) = 5 paces

B_y = (7 paces) (sin 45^o) = 5 paces

"West" means "to the left" or that the x-component is negative. The y-component is zero, so we have

C_x = - 10 paces

C_y= 0

"Northwest" means = 135^o, so

D_x = (7 paces) (cos 135^o) = - 5 paces

D_y = (7 paces) (sin 135^o) = + 5 paces

As always, watch the signs! They're important.

Now we're ready to add the component to find the components of the resultant. Vector notation is elegant shorthand notation. We write

R = A + B + C + D

but this means the following two ordinary, scalar equations:

R_x = A_x + B_x + C_x + D_x

and

R_y = A_y + B_y + C_y + D_y

For our example, these equations are

R_x = A_x + B_x + C_x + D_x

R_x = ( 5 + 5 - 10 - 5 ) paces = - 5 paces

or 5 paces to the west or to the "left" of the old oak tree (our origin).

and

R_y = A_y + B_y + C_y + D_y

R_y = ( 0 + 5 + 0 + 5) paces = 10 paces

or 10 paces north or "up" from the old oak tree ("up" meaning north, tho').

Now we can reconstruct the resultant R and its direction.

R = SQRT [ R_x² + R_y² ]

R = SQRT[ (- 5)² + (10)² ] paces

R = 11.2 paces

tan = ^opp / _adj = R_y / R_x

tan = ( 10 ) / ( - 5 ) = - 2

= 116.6^o

Remember, with our present coordinate system, this angle is measured from the positive x-axis. Let's talk about this angle itself. If you ask your calculator for the inverse tangent of - 2, it will probably tell you = - 63.4. But look at the diagram. You know that can not be right! What happened? There are two possible solutions,

= - 63.4^o

and

= - 63.4^o + 180^o

= 116.6^o

You and your diagram must decide which to use. Calculators are great; just be sure you control the calculator rather than the other way round (and that is even more true -- and often more difficult -- with computers!)!

Vector Properties			Unit Vectors
Return to ToC, Ch3, Vectors

(c) Doug Davis, 2001; all rights reserved