

We are often interested in how fast the velocity is changing. This is the acceleration.
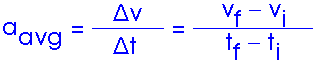
Acceleration is a change of velocity divided by a change of time so it has units of (meters/second)/second. We will write this as m/s/s or m/s2 (there are no "square seconds"). As with the velocity, we can describe the average acceleration or we can describe the instantaneous acceleration, the acceleration right now, at this particular moment,

This, too, is a derivative,
![]()
As with the velocity, we will usually mean the instantaneous acceleration if we simply say "the acceleration". We will often restrict ourselves situations with a constant acceleration; in that case the average acceleration is the same as the instantaneous acceleration.
![]()

![]()
We can take the definition of acceleration, turn it around,
and write
![]()
Disney's Rockin' Roller Coaster is catapulted from 0 to 60 mi/h in 2.8 s. What is its acceleration?
The distance an accelerating object moves is
x = xi + vi t + (1/2) a t2
If we need connections among distance, velocity, and acceleration -- for straight-line motion -- but do NOT need information about the time, we can also write
v2 = vi2 + 2 a (x - xi )
We now have the "Big Three Kinetmatics Equations":
![]()
x = xi + vi t + (1/2) a t2
v2 = vi2 + 2 a (x - xi )

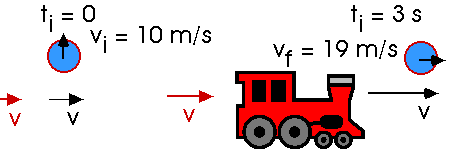
Consider a car that starts at rest and accelerates at 2 m/s/s for 3 seconds.
At that time, t = 3 s, how fast is it going? and how far has it gone?


|
|
|
 |
If a Jeep brakes to a stop, from 70 mph to zero, in 186 feet, what is its acceleration? (Caution: be careful of the units!) |
A certain sporty car claims that it does "zero to sixty (mi/h) in 6.2 s". How far has it traveled by then?
|
|
| ||
(c) Doug Davis, 2001; all rights reserved