

PHY1160C
Exam #4
December 7, 1999
Name: ___________________
Possibly useful information:
R = 1.097 x
107 m - 1 Subshells: l = 0, 1, 2,
3, . . .; s, p, d, f, g, h, . . . 1 u = 931
Mev/c2
![]()
![]()
![]()
![]()
![]()
![]()
![]() h
h
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() --->
---> ![]() +
+ ![]()
![]() --->
---> ![]() + b-
+
+ b-
+ ![]()
![]() --->
---> ![]() + b+
+ n
+ b+
+ n
First, some statistics:
High: 100 (several!)
Mean: 85
Low: 29
1. [25 pts] (27.2) A flashbulb goes off at the origins as the origins of our usual reference frames A and B coincide. Frames A and B have a relative speed of 0.6 c along their x-axes. A wavefront travels along the x-axis as observed in B. What time is recorded in B as this wavefront reaches xB = 1,000 m? Use these values of xB and tB to calculate the coordinates xA and tA that describe this event in A. Then use these values to calculate the speed of light in reference frame A ( vlight = xA/tA).
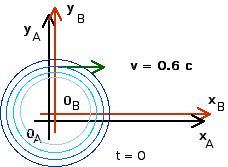
To find time tB we just use the definition of velocity
tB = xB/c
![]()
![]()
tB = 3.333 x 10 - 6 s
Of course, we also have
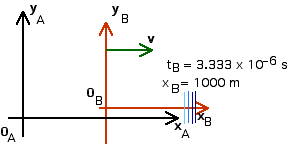
Now we can apply the Lorentz Transformations to find xA and tA,
![]()
![]()
![]()
![]()
xA = 2 000 m
![]()
![]()
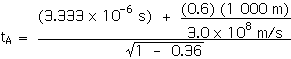
![]()
![]()
tA = 6.66 x 10 - 6 s
Now we can find the velocity in the A-frame and determine if the Lorentz Transformations work. Is it, indeed, true that the velocity of light will be the same in both frames? Let’s see, . . .
![]()
vA = 3.00 x 108 m/s
And, indeed, this is the speed of light!
2. [15 pts] (27.49) A spaceship travels away from Earth at a velocity of 2 x 108 m/s. A projectile is shot forward from the spaceship at 2.5 x 108 m/s relative to the spaceship. What is the velocity of the projectile relative to Earth?

This provides a more direct application of our velocity transformation equation,
with
vxMB = 2.5 x 108 m/s = (2.5/3) c
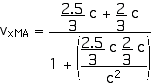
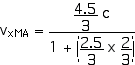
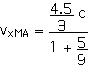

![]()
![]()
vxMA = 0.964 c
In the homework, I solved it as I have shown here -- with the fractions. You may feel more comfortable to simply plug in numbers directly. Then the solution goes like this:
with
vxMB = 2.5 x 108 m/s
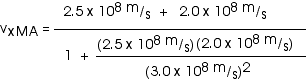
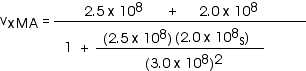
![]()

![]()
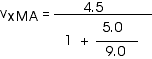
![]()
![]()
![]()
![]()
![]()
While it is fine to leave the velocity in this form, we could also write this as
![]()
And, except for some round-off error, that is exactly what we got earlier (as it must be, of course!)
3. [10 pts] (28.15) What is the energy of the photons in the visible region of the electromagnetic spectrum? (Use l = 550 nm as an average value)?
f l = c
f = c / l
E = h c / l
E = (4.14 x 10 - 15 eV s) (3.0 x 108 m/s) / 550 nm
E = (4.14 x 10 - 155 eV s) (3.0 x 108 m/s ) / 550 x 10 - 9 m
E = 2.26 eV
It seems easier, to me, to think of quantities like this in units of electron-volts. However, several people left this in Joules. Then, the solution looks like this:
f l = c
f = c / l
E = h c / l
E = ( 6.626 x 10 - 34 J s) (3.0 x 108 m/s) / 550 nm
E = (6.626 x 10 - 34 J s) (3.0 x 108 m/s ) / 550 x 10 - 9 m
E = 3.61 x 10 - 19 J
4. [15 pts] (28.41) What is the wavelength of an electron moving at 1.5 x 108 m/s (v = 0.5 c)?
l = h/p = h / mv
l = (6.626 x 10 - 34 J s) / [(9.11 x 10 - 31 kg)(1.5 x 108 m/s)]
l = 4.85 x 10 - 12 m
This wavelength is larger than a nuclear diameter and is a reasonable fraction of typical atomic spacing.
Balmer Series for Hydrogen
R = 1.097 x 107 m - 1, Rydberg constant
The first wavelength, or the first transition that this equation describes is for n = 3. Notice that n = 1 gives a negative value for the wavelength! This equation only describes the transitions from n = 3 to n =2, from n = 4 to n = 2, from n = 5 to n = 2, and so on.
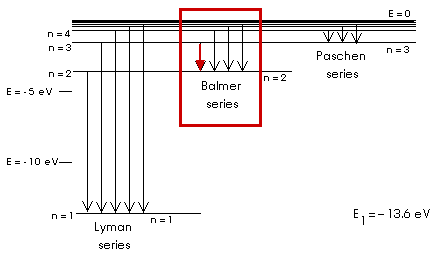
For n = 3 we have
= (1.097 x 107 m - 1) (0.2500 - 0.1111)
= (1.097 x 107 m - 1) (0.1389)
= 1.525 x 106 m - 1
ln=3 = 6.563 x 10 - 7 m
ln=3 = 656.3 x 10 - 9 m
ln=3 = 656.3 nm, and this is red light
(The red light from the HeNe laser I used in class has a wavelength of 634 nm).
6. [20 pts] (29.16) In state "A" the energy of an atom is - 3.45 eV and in state "B" its energy is - 5.67 eV.
a) What is the energy of the photon emitted in the transition from "A" to "B"?b) What is the wavelength of this photon?
c) What color is the light of this photon?
Ephoton = DE = EA - EB
Ephoton = ( - 3.45 eV) - ( - 5.67 eV)
Ephoton = 2.22 eV
E = hf = h(c/l)
l = hc/E
l = (6.626 x 10 - 34 Js)(3.0 x 108 m/s) / 2.22 eV
Be careful with the units! We need to convert E = 2.22 eV into units of J (or the equivalent) to finish carrying out this calculation
E = 3.55 x 10 - 19 J
l = (6.626 x 10 - 34 Js)(3.0 x 108 m/s) / 3.55 x 10 - 19 J
l = 5.60 x 10 - 7 m
l = 560 x 10 - 9 m = 560 nm
Perhaps an easier -- more direct method -- is to use h in units of eV-s,
E = hf = h(c/l)
l = hc/E
l = (4.14 x 10 - 15 eV s)(3.0 x 108 m/s) / 2.22 eV
Then the units of energy cancel directly,
l = {[(4.14 x 10 - 15)(3.0 x 108] / 2.22}{(s)(m/s)}
and, of course, the seconds cancel,
l = 5.60 x 10 - 7 m
l = 560 x 10 - 9 m = 560 nm
This is yellow light, near the middle of the range of visible light.
There are almost always various ways to arrive at the same, correct answer. That can be fun and interesting or, sometimes, frustrating!
(c) Doug Davis, 2002; all rights reserved