

deBroglie Waves
Consider Physics of the 1920's for a moment. Light, that was "well known" to be a wave, behaved as a particle. The electron was "clearly" a particle -- Millikan had recently measured its charge and, thus, its mass for the ratio of e/m had been known for over two decades. In 1923, while still a graduate student, Louis deBroglie made a bold -- even outrageous -- proposal. Appealing to symmetry of nature, deBroglie proposed that electrons, too, have a wave nature and a wavelength! deBroglie proposed that all material objects have a wave nature. In particular, deBroglie proposed that the wavelength of a body could be found from
or
where h is again Planck's constant, p is the momentum, m is the mass, and v is the speed of the object. This wave associated with a body is often called its deBroglie wave. Planck's constant h has such an extremely small value that the wavelength associated with any ordinary object is far too small to be experimentally detected.
What is the deBroglie wavelength of an 1100-kg automobile moving at 10.0 m/s?
The deBroglie wavelength is given by our equation above.
Solution:
=
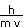
=
= 6.03 x 10-38 m
The diameter of an atomic nucleus is only about 10 - 14 m so a wavelength of 10-38 m is immeasurably small! We can never expect to measure anything this small.
What is the deBroglie wavelength of a 20 keV electron? Such electrons are typical in the "electron guns" of color TVs or color computer monitors.
We know the kinetic energy of the electron to be 20 keV but we need its momentum mv to find its deBroglie wavelength. We can solve for the momentum from the kinetic energy.
Solution:
KE = (1/2)m v2 This can be restated in terms of the momentum
KE = p /2m And we can solve for the momentum
p2 = 2 m KE Putting in numerical values, we find
p2 = 2 (9.11 x 10 - 31 kg)(20 x 103 ev) [ 1.60 x 10 - 19 J / ev ] p2 = 5.83 x 10 - 45 [ kg m / s ]2
or
p = 7.64 x 10 - 23 kg m / s That may seem like a very small number. And it is if we compare it to the momentum of the car in the previous example or a baseball or even a slowly-moving ping-pong ball. But we are going to use this in a calculation with Planck's constant h which also seems very small when compared to ordinary objects.
= h / p
= 6.626 x 10 - 34 J s / 7.64 x 10 - 23 kg m/s
= 8.67 x 10 - 12 m
This number is small compared to the proverbial breadbox but it is about the size of atomic spacings -- about 100 times as large -- so we might be able to actually measure this wavelength. Indeed, electron diffraction from crystals experimentally verifies this wave-nature of the electron!
Compton Scattering Complementarity Return to Ch 28, Quantum Mechanics (c) Doug Davis, 2002; all rights reserved