

The Lorentz Transformations
The Galilean Transformations do not give the experimentally observed results that all inertial observers measure the same value for the speed of light. If they are wrong, what are the correct transformations?
Consider our usual situation of two observers--or two reference frames--which pass each other, moving along the common direction of their x-axes. As the two origins concide, the two observers set their clocks to zero.
Consider a point P. Observer B records its x-coordinate as xB while observer A records its x-coordinate as xA. How are these related? Our intuition tells us that
xA = v t + xB But that is just the Galilean transformation equation and we already know that is wrong.
Being more careful, we can write
xA = v tA + f xB where f is a "distortion factor" that we introduce because we know there must be something "unusual" going on with distances measured by these moving observers.
Now look at this same point P from Observer B's viewpoint,
Now we can write
f xA = v tB + xB We know that both A and B will observe the same speed of light, so let P be a point on a crest of a light wave that started at the common origin when tA = tB = 0. Then
xA = c tA and
xB = c tB For this situation, our earlier equations become
c tA = v tA + f (c tB) f (c tA) = v tB + (c tB)
or
c tA - v tA = f c tB f c tA = (c + v) tB
(c - v) tA = f c tB
f c tA = (c + v) tB
Dividing one by the other, the times cancel, and we are left with
or
f2 c2 = (c - v) (c + v) = c2 - v2 f2 = 1 - v2/c2
Thus, the "distortion factor" f is
f = SQRT ( 1 - v2/c2) or
This allows us to write
We can solve for the time tA, to write
Or, we can solve for xB and tB to get the inverse transformations:
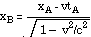
tB =
These are known as the Lorentz transformations. For v << c, they reduce to the earlier Galilean transformations as, indeed, they must. Notice, further, that while the equations for xB and tB are easy to arrive at algebraically; we can get them by symmetry. Interchanging the roles of A and B is the same as replacing v with - v!
So far we have not mentioned the coordinates y and z, perpendicular to the relative velocity vector. They are not altered at all. That is,
yB = yA and
zB = zA Now that we have the Lorentz Transformations, what do they mean or what can we do with them?
If we know the SpaceTime coordinates of an event as measured by observer A, we can calculate the SpaceTime coordinates for that same event that will be measured by observer B. That is, if we know (xA, yA, zA, tA), the Lorentz Transformations allow us to calculate (xB, yB, zB, tB). Of course, we can go the other way as well. If we start with B's measurements of (xB, yB, zB, tB), the Lorentz Transformations allow us to find A's measurements (xA, yA, zA, tA).
Return to Ch 27, Special Relativity (c) Doug Davis, 2002; all rights reserved