Galilean Relativity

Consider two observers, A and B, moving relative to each other. How can we compare their observations?

In particular, consider two reference frames, labeled A and B, which move relative to each other with constant velocity v, oriented so they are parallel and their x-axes align with their relative velocity. The velocity of frame B relative to A is v and the velocity of frame A relative to B is - v. Further, to simplify matters, we start our clocks or stopwatches when the origins of the two reference frames coincide. All this is shown schematically here.

 

Now consider an object located at point P. Observers in both frames record its position and velocity. Of course, they get different numbers. but these numbers can be related to each other by using these transformation equations:

xA = xB + vt

yA = yB

vAx = vBx + v

vAy = vBy

where xA and yA are the coordinates of point P measured by observer A while xB and yB are the coordinates measured by observer B; vAx, and vAy are the components of P's velocity measured by A, and vBx and vBy are the velocity components measured by B. Everybody measures t for the time and v is the relative speed of the two observers. These equations are the Galilean Relativity Transformations. The position equations may be combined and written in vector form as

rA = rB + v t

while the velocity equations may be combined and written in vector form as

 

vA = vB + v

All these transformation equations may be seen in the following schematic diagram:

 

Table of Contents

More Diagrams
Return to Ch 27, Special Relativity
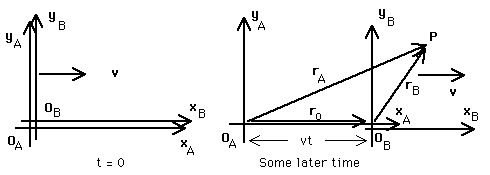
(c) Doug Davis, 2002; all rights reserved