Homework

Chapter 27: Special Relativity

Ch 26: 1, 2, 4, 9, 10, 18, 20, 46, 49, 51, 60, 63, 82

 

27.1 Frame B moves relative to frame A with a relative speed of 0.8 c along the common direction of their x-axes. All clocks read zero as the origins coincide. An observer in B sees an explosion (an event) on her x-axis at position x_B = 1.5 km and at time t_B = 0.001 s. When and where does A observe this event?

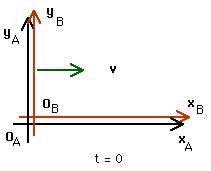
This calls for a direct application of the Lorentz Transformations:

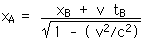
x_B = 1.5 km = 1.5 x 10³ m

v = 0.8 c = 0.8 x 3 x 10^{8 m}/_s

t = 0.001 s

x_A = 4.025 x 10⁵ m

t_A = 0.001673 s

 

27.2 A flashbulb goes off at the origins as the origins of our usual reference frames A and B coincide. Frames A and B have a relative speed of 0.6 c along their x-axes. A wavefront travels along the x-axis as observed in B. What time is recorded in B as this wavefront reaches x_B = 1,000 m? Use these values of x_B and t_B to calculate the coordinates x_A and t_A that describe this event in A. Then use these values to calculate the speed of light in reference frame A ( v_light = x_A/t_A).

To find time t_B we just use the definition of velocity

v = c = x_B/t_B

t_B = x_B/c

t_B = 3.333 x 10 ^{- 6} s

Of course, we also have

x_B = 1000 m

Now we can apply the Lorentz Transformations to find x_A and t_A,

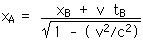
x_B = 1 000 m

v = 0.6 c = 0.6 x 3.00 x 10⁸ m/s

t_B = 3.333 x 10 ^{- 6} s

x_A = 2 000 m

t_A = 6.66 x 10 ^{- 6} s

Now we can find the velocity in the A-frame and determine if the Lorentz Transformations work. Is it, indeed, true that the velocity of light will be the same in both frames? Let's see, . . .

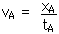
v_A = 3.00 x 10⁸ m/s

And, indeed, this is the speed of light!

 

27.4 Two events in frame B occur with coordinates (x_B, y_B, z_B, t_B). For event E₁ the values are (100 m, 0, 0, 3 x 10 ^{- 7} s) and for event E₂ (200 m, 0, 0, 5 x 10 ^{- 7} s). Frame B moves past frame A at 0.7c along their common x-axes. Find the coordinates of E₁ and E₂ measured by A.

 

This requires a direct application of the Lorentz Transformations,

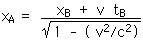
y_A = y_B

z_A = z_B

We begin with event E₁,

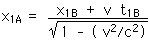
x_1A = 228.2 m

y_1A = y_1B = 0

z_1A = z_1B = 0

t_1A = 7.468 x 10 ^{- 7} s

 

Now we do exactly the same for the coordinates of event E₂,

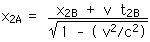
x_2A = 427.1 m

y_2A= y_1B = 0

z_2A = z_1B = 0

t_2A = 1.354 x 10 ^{- 6} s

 

27.9 An alien spaceship moving at v = 0.6 c travels north from Los Angeles toward Vancouver. The captain and first officer, standing at the bow (front) and stern (rear), 500 m apart, sneeze at precisely the same time -- as observed by their crew. What time difference between their sneezes will be measured by Earth-based observers? Who will be seen to sneeze first?

Consider Earth the A-frame and the "moving" spaceship, the B-frame. In the frame of reference of the spaceship (in the B-frame), the two events are simultaneous, meaning

t_B = 0

t_A = 1.25 x 10 ^{- 6} s = 1.25 s

Events on the "leading edge" of a moving reference frame are observed to occur earlier. Therefore, the captain located at the bow will be observed to sneeze 1.25 s earlier than the first officer located at the stern.

  

27.10 A space traveler whizzes past Earth at a speed of 0.75 c. As her clock indicates a passage of 100 seconds, how much time elapses on Earth? What length will Earth-based observers measure for the length of her spaceship if it is 100 m long at rest?

These questions ask for the Einstein time dilation and the Lorentz-Fitzgerald contraction. A clock -- or wrist watch -- moving with the space traveler measures the "proper time" t_o while the Earth-bound observer measures time t.

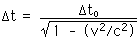
t = 151.2 s

L = (100 m)(0.6614)

L = 66.14 m

 

27.18 A rocket goes past a space station with a speed of 0.970 c. A light on the nose of the rocket flashes as it passes. According to the astronaut in the rocket, the duration of the light flash is 2.5 ms. What is the duration of the flash according to an astronaut in the space station?

As measured by the astronaut at rest wrt the light, the light comes on for 2.5 ms. That means this 2.5 ms is the "proper time" and we can apply the equation for the Einstein time dilation.

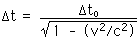
t = 10.28 ms

 

27.20 A railroad train at rest in a yard is carefully measured to have a proper length of precisely 1.00 km. What will be its length, measured by observers at rest on Earth, if it travels at 100 km/hr? if it travels at 100,000 km/hr? if it travels at 100,000,000 km/hr?

We know the speed of light at c = 3.00 x 10⁸ m/s so we must first convert all these speeds to units of m/s.

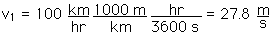
Now we can apply the Lorentz-Fitzgerald contraction,

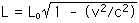
L₁ = L_o (0.999 999 999 999 995 72) 

That means that L₁ = L_o (or L₁ = 1.00 km) to fifteen significant figures!

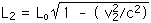
L₂ = L_o (0.999 999 995 72)

That means that L₂ = L_o (or L₂ = 1.00 km) to nine significant figures.

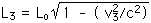
L₃ = L_o (0.995 72)

L₃ = (1,000 m)(0.995 72)

L₃ = 995.72 m

Only now, at this extremely high speed of 100,000,000 km/hr, do we find a reasonably measureable difference in the length!

  

27.46 Two particles are moving in the same direction along the x-axis, particle 1 at 0.6 c and particle 2 at 0.8 c. What is v₂₁, the speed of particle 2 as seen by 1?

[[ Problem 27.49 is also a velocity-transformation question. However, it is more direct. Be sure to look at 27.49 before you work this problem. That will help in understanding this one! ]]

We have a velocity transformation equation,

We can use this equation if we let particle 1 be the B reference frame

 

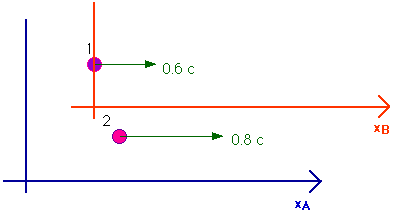
and set

v_xMA = 0.8 c

v = 0.6 c

v_xMB = v₂₁

Then

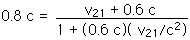
(0.8 c)[1 + 0.6 v₂₁/c] = v₂₁ + 0.6 c

0.8 c + 0.46 v₂₁ = v₂₁ + 0.6 c

0.54 v₂₁ = 0.2 c

v₂₁ = 0.37 c

 

27.49 A spaceship travels away from Earth at a velocity of 2 x 10⁸ m/s. A projectile is shot forward from the spaceship at 2.5 x 10⁸ m/s relative to the spaceship. What is the velocity of the projectile relative to Earth?

This provides a more direct application of our velocity transformation equation,

with

v = 2 x 10⁸ m/s = (²/₃) c

v_xMB = 2.5 x 10⁸ m/s = (^2.5/₃) c

v_xMA = 0.964 c

 

27.51 In pair production, gamma rays produce an electron and a positron. Consider the situation in which these two particles move away from their point of creation, in exactly opposite directions, each with a speed of 0.95 c, relative to the laboratory reference frame. What is the speed of one with respect to the other?

This provides another application of our velocity transformation equation,

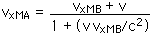
Describe particle 1 as the "moving" reference frame B. Then

v = 0.95 c

The velocity of particle 2 as seen in the LAB frame is the velocity of M as seen in the "stationary" frame A; that is,

v_xMA = - 0.95 c

And we are looking for the velocity of particle 2 as seen by particle 1. In terms of our velocity transformation equation, that is the velocity of M as seen by the "moving" frame B,

v₂₁ = v_xMB

then becomes

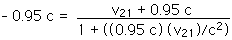
[- 0.95 c][1 + 0.95 v₂₁/c] = v21 + 0.95 c

- 0.95 c - 0.9025 v₂₁ = v₂₁ + 0.95 c

1.9025 v₂₁ = - 1.9000 c

v₂₁ = - 0.9987 c

 

27.60 What is the mass of an electron (m_o = 9.11 x 10 ^{- 31} kg) traveling at 0.999 c?

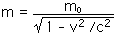
m = 2.038 x 10 ^{- 29} kg

 

27.63 How fast must an object travel if its mass is to increase by one percent?

m = 1.01 m_o

1 - v²/c² = ( 0.9901 )² = 0.9803

v²/c² = 1 - 0.9803 = 0.0197

v² = 0.0197 c²

v = 0.14 c

That is, traveling at 14% the speed of light causes a 1% mass increase (and a 1% length contraction and a 1% time dilation).

  

27.82 An astronaut of the future has a height of 2.0 m, a mass of 80 kg, and a heart rate of 75 beats per minute when examined at rest on the ground before leaving. The trip to a distant star is along a straight line at 0.85 c. What values for height, mass, and heart rate are measured by Earth-based observers during the trip?

We will also assume that the straight line of the trip is parallel to the astronaut's height. The heart rate is given in units of beats per minute. We need a time period,

t_o = 1/f = (1/75) min = 0.0133 min

Now we are ready to calculate the values observed by the Earth-based frame while the astronaut travels at v = 0.85 c.

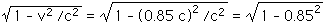
For the astronaut's measured height (or length),

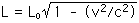
L = (2.0 m)(0.527)

L = 1.054 m 

For the astronaut's measured mass,

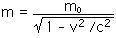
m = 80 kg/0.527

m = 151.8 kg

For the astronaut's measured heart rate,

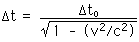
t = 0.0253 min

f = 1/t

f = 39.6 beats per minute (heart rate)

Summary			Ch 28, Quantum Mechanics
	Return to Ch 27, Special Relativity (ToC)

(c) Doug Davis, 2002; all rights reserved