Homework

Chapter 26: Optical Instruments

Ch 26: 2, 3, 5, 9, 13, 15, 20, 25, 27

| Return to Ch 26 Home Page (ToC) |

26.2 A pin-hole camera is used to take a photograph of a student who is 1.8 m tall. The student stands 2.7 m in front of the camera. Film is placed 10 cm behind the pin-hole. Determine the height of the image produced.

The triangle formed by the object (the student) and the rays from the student's head and feet going to the pin-hole and the triangle formed by the image and the rays coming from the pin-hole toward the head and feet of the image are similar triangles so the ratios of corresponding sides of these triangles are equal. That is,

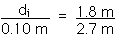
d_i = 0.067 m = 6.7 cm

 

26.3 The distance from the cornea to the retina of some particular eye is 2.1 cm. Find the effective focal length of this eye for an object located

(a) at infinity,

(b) for an object located 10 m away, and

(c) for an object located 25 cm away.

We can directly apply the Image Equation

The image distance, di, is the distance from the cornea to the retina, 2.1 cm.

For (a), the object distance, d_o, is infinite,

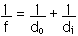
f = 2.1 cm

For (b), the object distance is d_o = 10 m

Watch the units! You can not add meters and centimeters; you can not add inverse meters and inverse centimeters. The two terms on the right must have the same units before you can add them!

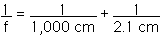
f = 2.096 cm 2.1 cm

For (c), the object distance is d_o = 25 cm

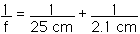
f = 1.94 cm

 

26.5 An object sits 35 cm to the left of a converging lens with focal length of 20 cm. 75 cm to the right is a second converging lens with focal length of 15 cm. Locate and characterize the final image.

A ray diagram is always a good way to start. There is usually more real understanding available in the ray diagram than in "merely" solving the problem numerically. In addition, a good diagram also provides a place to keep all the dimensions of the problem.

For the first lens, we begin with the Image Equation,

or

And we know f₁ = 20 cm and d_o1 = 35 cm,

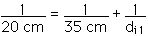
d_i1 = 46.7 cm

This image (which is real, inverted, and enlarged) becomes the object for the second lens as we again apply the Image Equation,

or

Since the lenses are 75 cm apart, the image formed 46.7 cm to the right of lens #1 is located 28.3 cm to the left of lens #2 so the object distance, then, is

d_o2 = 28.3 cm

d_i2 = 31.9 cm

That is, the final image is located 31.9 cm to the right of the second lens. Since d_i2 > 0 (that is, since d_i2 = +), we know this image is real. It is inverted, compared to the object for lens #2. But that was an inverted image of the original object. Therefore, this final image is upright.

The total magnification is the product of the magnifications of the two lenses,

M_tot = M₁ M₂

M_tot = (1.33)(1.13)

M_tot = 1.5

 

26.9 A patient's eye can focus only on objects beyond 100 cm. What word characterizes this type of vision problem? What are the focal length and power of the contact lens needed to correct this problem?

This patient is farsighted or hyperopic. This patient has trouble reading a book at a comfortable distance -- such as 25 cm -- so we must find a lens that will take an object at 25 cm (d_o = 25 cm) and create an image (a virtual image) at 100 cm (d_i = - 100 cm).

A diagram may help to clearly establish that we need

d_o = 25 cm

d_i = - 100 cm

It is important to remember or realize that the image formed is a virtual image. It is on the left side of the lens in the diagram above. This means the image distance is negative. Once we know do and di then it is easy to find the focal length of the lens from the Image Equation,

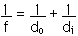
f = 33.3 cm

To describe the lens in terms of "power" (in units of diopters) we need to take the inverse of its focal length in meters,

f = 0.3 m

P = 1/f = 3 diopters

 

26.10 A certain eye can focus only on objects closer than 50.0 cm. What word characterizes this type of vision problem? What sort of contact lens (described both in focal length and power) will correct this problem?

This eye is myopic or nearsighted. We need to find a lens that will take an object at infinity (d_o = ) and produce a virtual image at 50.0 cm (d_i = - 50.0 cm = - 0.50 m).

Now we know the image and object distances --

d_o =

d_i = - 50.0 cm

It is important to remember or realize that the image formed is a virtual image. It is on the left side of the lens in the diagram above. This means the image distance is negative. Once we know d_o and d_i then it is easy to find the focal length of the lens from the Image Equation,

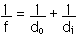
f = - 50.0 cm

f = - 0.50 m

P = ¹/_f = - 2 diopters

Note: This problems started out in the book with a far point of 500 cm or 5.0 m. As we will see, that does not require very much correction to be able to see something at infinity. This does not seem like a reasonable or interesting problem. Therefore, I changed the problem. However, let's go ahead and solve this for the original case --

d_o =

d_i = - 500 cm

f = - 500 cm = - 5 m

P = 0.20 diopters

 

26.11 A particular eye can focus only on objects more distant than 150 cm. What word characterizes this type of vision problem? What are the focal length and power of the corrective lens needed to correct this problem? The lens is to be worn 2.0 cm in front of the eye?

Using a lens that is 2 cm from the eye is but a slight variation from problem 26.9 that used a contact lens. For this situation we have

d_o = 23 cm

d_i = - 148 cm

It is important to remember or realize that the image formed is a virtual image. It is on the left side of the lens in the diagram above. This means the image distance is negative. Once we know do and di then it is easy to find the focal length of the lens from the Image Equation,

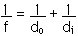
f = 27.2 cm = 0.272 m

P = ¹/_f = 3.7 diopters

 

26.20 A diamond is viewed with a jeweler's loupe that has a focal length of 5.0 cm. Where must the diamond be placed to provide a virtual image at infinity? What will be the angular magnification of this simple magnifier?

The diamond should be placed at the focal point of the lens (the jeweler's loupe), that is, 5.0 cm from the lens.

The magnification is given by

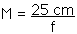
M = 5

 

26.25 A microscope has its objective and eyepiece 18 cm apart. If f_obj = 0.40 cm and f_eye = 5.0 cm, where must a specimem be located to produce a final virtual image at infinity? What is the total magnification of this microscope?

To have the final image at d_i = °, we need the real image formed by the objective to be located at the focal point of the eyepiece. With the objective and eyepiece lenses 18.0 cm apart this means,

d_i + f_eye = 18.0 cm

d_i + 5.0 cm = 18.0 cm

d_i = 13.0 cm

Now we can again apply the Image Equation,

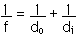
d_o = 0.41 cm

 

26.27 An astronomical telescope is used to view an object at infinity. The objective lens has a focal length of 15.0 cm. Where must the 0.5 cm eyepiece be placed to form an image at infinity? What is the total angular magnification?

The real image formed by the objective lens will be located at the focal point for that lens, d_i = f_obj = 15.0 cm from that lens. To produce a virtual image at infinity, the eyepiece must be located so that this image -- which acts as an object for the eyepiece -- is located at the focal point for the eyepiece lens, d_o = f_eye = 0.5 cm.

Therefore, the eyepiece must be 15.5 cm from the objective lens.

The total magnification is given by

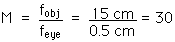
M = 30 

Summary			Ch 27, Special Relativity
	Return to Ch 26 Home Page (ToC)

(c) Doug Davis, 2003; all rights reserved