Ch 25 Homework

Ch 25: 5, 17, 28, 40, 44, 62, 63

25.5 Two slits 0.03 mm apart are illuminated by parallel rays and the 5th-order maximum is 14 cm from the central bright maximum on a screen 2.0 m from the slits. What is the wavelength of the light falling on the slits?

Maxima (or bright fringes) occur for

d sin = m

We can solve this for

= (d sin ) / m

We can solve for or sin from

tan = ^opp/_adj = ^{14 cm}/_{200 cm} = 0.07

= 4.00°

sin = sin 4.00° = 0.07

d = 0.03 mm = 3 x 10 ^{- 5} m

Therefore

= [(3 x 10 ^{- 5} m)(0.07)] / 5

= 4.2 x 10 ^-7 m = 420 x 10 ^{- 9} m = 420 nm

 

25.17 Red light ( = 640 nm) passes through a diffraction grating and on to a screen 2.0 meters away. There the first-order maximum or bright line appears 25 cm on either side of the central maximum. How many lines per centimeter are there on the grating?

First, determine the angle ,

tan = ^{25 cm}/_{200 cm} = 0.125

= 7.125°

We expect to find maxima or bright regions for

d sin = m

Here we have only first-order maxima, with m = 1, on either side of the central maximum (m = 0) so we can solve for d, the separation distance between the "slits" of the diffraction grating,

d = m / sin = / sin

d = 640 nm / sin 7.125°

d = 640 nm / 0.124

d = 5160 nm = 5,160 x 10 ^{- 9} m = 5.16 x 10 ^{- 6} m

d = 5.16 x 10 ^{- 4}cm

This is the slit separation distance. From this we can determine N the number of slits there are in a centimeter. If there were ten slits per centimeter (N = 10/cm) then the separation distance would be 0.1 cm (d = 0.1 cm). N and d are related by

N = 1/d

N = 1.94 x 10³ lines/cm = 1,940 lines/cm

 

25.28 When 634-nm light passes through a slit 0.1 mm wide and forms a diffraction pattern on a screen 1.25 m away, what is the distance from the central maximum to the center of the first minimum?

For a single-slit diffraction pattern, the first minimum occurs for

D sin =

or

sin = /D

sin = 634 nm/0.1mm

sin = ( 634 x 10 ^{- 9} m ) /( 0.1 x 10 ^{- 3} m)

sin = 6.34 x 10 ^{- 3} = 0.00634

The distance y is given by

tan = ^y/_L

where L is the distance from the slit to the screen, L = 1.25 m

y = L tan

For such small angles

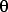
tan sin

y = L sin

y = (1.25 m)(0.00634)

y = 7.93 mm

 

25.40 A high precision telescope advertises that it can resolve the eyes of a bird (assume them 1 cm apart) at 1.5 km. What is the minimum objective diameter?

The Rayleigh criterion for rsolution of two point sources is

= 1.22 / D

D = 1.22 /

tan = 1.0 cm / 1.5 km = 1.0 x 10 ^{- 2} m / 1.5 x 10³ m

tan = 6.67 x 10 - 6

= 6.67 x 10 ^{- 6} radians (= 3.8 x 10 ^{- 4} degrees)

Since no particular wavelength is given for the light, use a wavelength near the middle of the visible spectrum such as

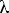
550 nm = 550 x 10 ^{- 9} m

D = 1.22 /

D = 1.22 ( 550 x 10 ^{- 9} m) / 6.67 x 10 ^{- 6}

D = 10 cm

 

25.44 Magnesium chloride (MgCl₂), which has an index of refraction of 1.25, is often used for the non-reflecting coating on photographic lenses. How thick must a film of it be to have total destructive interference for 560 nm light?

For a thin film like this, with n₁< n₂ and n₂< n₃, total destructive interference occurs for

2 t = [ m + (1/2)] ' = [ m + (¹/₂)] / n

m is an integer. For the thinnest film, m = 0.

2 t = (¹/₂)(560 nm) / 1.25

t = (¹/₂)(560 nm) / [ (1.25) (2) ]

t = 112 nm

t = 1.12 x 10 ^{- 7} m

 

25.62 When 580-nm light passes through a 1500 line/cm diffraction grating, how many orders of maxima do you see on a screen that is 1.5 m wide and1.2 m from the grating?

Recalling, from Problem 25.28, that d = ¹/_N, we can determine the slit separation distance d from N, the number of lines/cm,

d = 6.67 x 10 ^{- 6} m

Maxima for diffraction patterns occur for

d sin = m

The largest possible angle _max is

tan _max = 1.5 m / 1.2 m = 1.25

_max = 51.3°

sin _max = 0.78

Then the largest possible order m_max is given by

m = d sin /

m_max = d sin _max /

m_max = (6.67 x 10 ^{- 6} m)(0.78) / (580 x 10 ^{- 9} m)

m_max = 8.97

But m must be an integer! What does m_max = 8.97 mean? The maximum order of diffraction pattern (bright area) that we will see will be

m = 8

The next bright diffraction pattern, for m = 9, will be just off the edge of the screen.

 

25.63 An observer looks at a light source through a grating having 1000 lines/cm. If = 500 nm, how many images of the source can be seen? (Hint: For what order is = 90 degrees?)

Of course, this is similar to the previous problem. We can determine the slit separation distance d from N, the number of lines/cm,

d =1.0 x 10 ^{- 5} m

Maxima for diffraction patterns occur for

d sin = m

The largest possible angle _max is 90° or sin _max = 1.0

m_max = d sin _max /

m_max = (1.0 x 10 ^{- 5} m) (1.0) / (500 x 10 ^{- 9} m)

m_max = 20

 

 

Summary			ToC, Ch 26, Optical Instruments
Return to Ch 25, Wave Optics: Interference and Diffraction

(c) Doug Davis, 1997; all rights reserved