Chapter 24: Mirrors and Lenses
Ch 24: 3, 7, 17, 24, 29, 43, 73

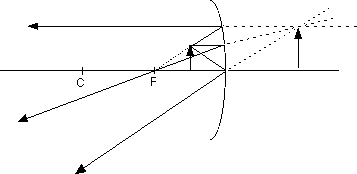
24.3 Locate and describe your own image when you look into a make-up mirror whose radius is 1.0 m when you hold it 25 cm in front of your face.

Always start with a clear ray diagram; this is more useful to understanding than just solving the equation. Always ask if the solution to the equation is consistent with your ray diagram.

Now we are ready for the "image equation",

The focal length is one-half the radius of curvature

Your face is the object so the object distance is d_o = 25 cm

d_i = - 50 cm

The negative sign means this is a virtual image.
We can find the magnification from

The magnification is M = 2. This positive magnification means the image is upright. Since M > 1, the image is enlarged.


24.7 A dentist holds a concave mirror of radius of curvature 50 mm at a distance of 20 mm from a cavity in a tooth. Where is the image of the cavity and how large is it?
From the radius of curvature, we know the focal length,

The object distance is

Now we can calculate the image distance,

d_i = - 100 mm
The negative sign means this is a virtual image.

(Ray diagrams are still important. The ray diagram for this would look similar to the one for the previous problem).

We now find the magnification by

The image of the cavity is five times the real cavity (and the image is upright). It is also a virtual image.


24.17 A man standing 1.52 m in front of a shaving mirror produces an inverted image 18.0 cm in front of it. How close to the mirror should he stand if he wants to form an upright image of his chin that is twice the actual size of his chin?
The initial information about object distance and image distance lets us determine the focal length of the mirror --

Notice that d_i = + 18 cm since the image is in front of the mirror (and since it is inverted). The fact that d_o = 152 cm should be easy.

f = 16.1 cm = 16 cm
To form an upright image means M > 0; to have an image twice the size of the object (or chin) means M = 2. Either also requires a virtual image. Thus,

d_i = - 2 d_o

Essentially, we have two equations with two unknowns,

2 d_o = 16 cm
d_o = 8 cm

24.24 If you look at your toes while standing in 1.0 m of water, how far below the surface will they appear to be?

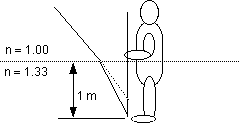
The apparent depth is given by

d_i = 0.75 m = 75 cm

24.29 A light 5.0 cm tall is held 30 cm in front of a converging lens with focal length of 24.0 cm. Locate and describe the image.
Again, a ray diagram will be very useful.

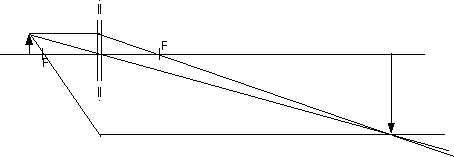
From the ray diagram we know the image is

The image distance can be approximated as about 120 cm or so.
Now we are ready to do the actual calculations,

d_i = 120 cm

(My estimate was unusually close!)

The positive value for the image distance means it is a real image.

The image is four times the size of the object, and inverted.

24.43 a) How far from a converging lens of focal length 60 cm must an object be placed if the image is to be real and four times as large as the object?
b) Repeat the calculation for a virtual image.
Knowing the magnification gives us an equation relating d_i and d_o,

d_i = M d_o
d_i = (- 4) d_o

The magnification for a real image is negative.
Now we can apply the image equation or the thin lens equation,

d_o = 45 cm

For the virtual image of part b), the magnification will be positive, meaning the image is also upright. Therefore,

24.47 An astronaut in a space lab focuses a 60 mm focal length camera lens to form a sharp image of Earth. How far must she move the lens (and will it be toward or away from the film) in order to focus on a fellow astronaut, 3.0 m away?
Earth is essentially infinitely far away from the lens so d_o = °. We can then calculate the initial image distance d_i1.

d_i1 = 60 mm

Now we calculate the image distance d_i2 when the object distance is d_o = 3.0 m = 3,000 mm,

d_i2 = 61.20 mm

The difference in these two is the amount by which the distance from camera lens to film plane must be changed,

d_i = 1.20 mm

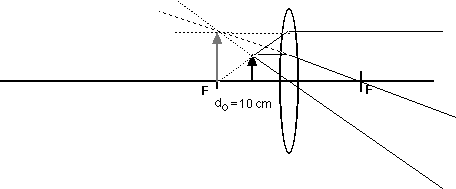
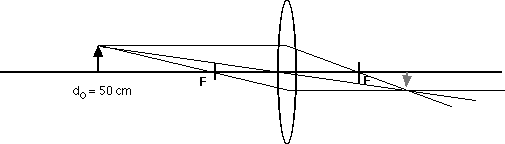
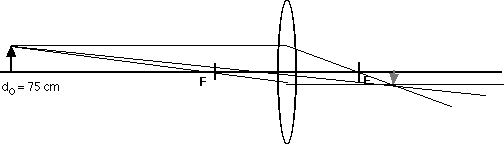
24.73 An object is placed to the left of a 20 cm focal length lens. Where is the image formed as the object is moved to the following object distances?

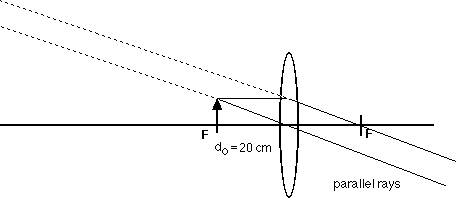
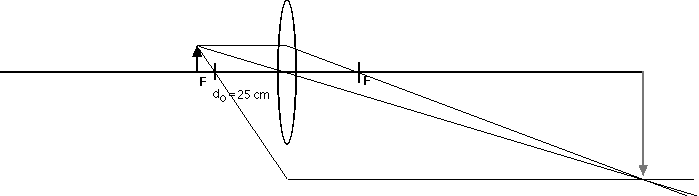
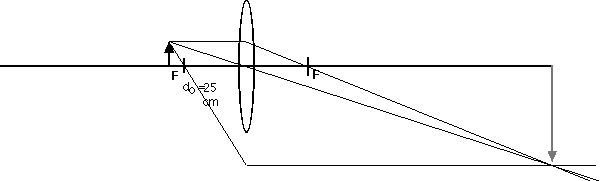
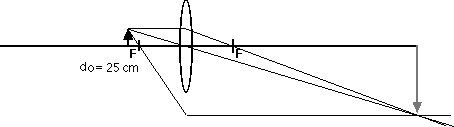
d_o = 10 cm, 20 cm, 25 cm, 50 cm, 75 cm

This requires the same type of calculation to be done several times. In a case like this, it is better or more efficient to solve this once symbolically and then put numbers into the resulting equation.

At this point, it is easy and efficient (altho’ not at all necessary) to put this into a small spreadsheet&emdash;

As always, it is interesting and useful to compare these calculated results with ray diagrams.

Summary			Ch 25, Wave Optics
Return to PHY 1160's Home Page

(c) Doug Davis, 2002; all rights reserved