PHY 1161C

Homework

Chapter 23: Reflection and Refraction of Light

Ch 23: 8, 10, 14, 20, 26, 28, 33, 38, 43, 45, 52 

  

23.8 What is the speed of light in water (n = 1.33)?

n = c/v

v = c/n

v = (3.00 x 10^{8 m}/_s)/(1.33)

v = 2.26 x 10^{8 m}/_s

 

23.10 What is the wavelength in water of blue light, with a wavelength of 440 nm in air?

[Visible light has wavelengths from about 700 nm for red light to about 400 nm for violet light].

v = f for all waves

c = f _o for light in air

v = f ’ for light in water

Divide one of these by the other to obtain

’ = _o/(c/v)

’ = _o/n

’ = ^{440 nm} / _1.33

’ = 330 nm

23.14 Two light pulses are emitted simultaneously from a source. Both pulses travel to a detector over the same physical distance but one passes through 6.2 cm of ice. What is the difference in the pulses' times of arrival at the detector?

The index of refraction for ice is 1.305

The time for the light to travel a distance of 6.2 cm = 0.062 m through the ice is

t = d/v

v = c/n

v = (3.00 x 10⁸ m/s)/1.305

v = 2.299 x 10⁸ m/s

t_ice = 0.062 m/(2.299 x 10⁸ m/s)

t_ice = 0.0270 x 10 ^{- 8} s

The time for the other light beam to travel a distance of 6.2 cm = 0.062 m through the air is

t = d/v

v = 3.00 x 10⁸ m/s

t_air = 0.062 m/(3.00 x 10⁸ m/s)

t_air = 0.0207 x 10 ^{- 8} s

The difference in these two times is

t = t_ice - t_air = 0.0063 x 10 ^{- 8} s

t = 0.063 x 10 ^{- 9} s = 0.063 ns

 

23.20 A SCUBA diver, underwater, shines a light up toward the smooth surface of the water with an angle of incidence of 35°. At what angle does the light leave the water?

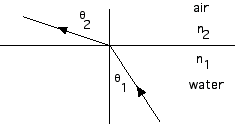
We begin with Snell’s law,

n₁ sin ₁ = n₂ sin ₂

(1.33)(sin 35°) = (1.00) sin ₂

(1.33)(0.5736) = (1.00) sin ₂

sin ₂ = 0.7269

₂ = 49.7°

 

23.26 An aquarium with glass walls (n = 1.50) is filled with water (n = 1.33). A ray of light, passing through the air strikes the glass side with an angle of incidence of 37°. What is the angle of refraction inside the water?

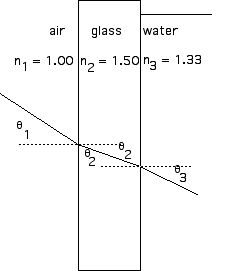
We can apply Snell’s Law twice,

n₁ sin ₁ = n₂ sin ₂

n₂ sin ₂ = n₃ sin ₃

n₁ sin ₁ = n₃ sin ₃

(1.00) sin 37° = (1.33) sin ₃

(1.00) (0.60) = (1.33) sin ₃

sin ₃ = 0.60/1.33 = 0.452

₃ =26.9°

23.28 A SCUBA diver, underwater, shines a light up toward the smooth surface of the water with an angle of incidence of 53°. Explain what happens to the light.

The critical angle for total internal reflection at the water-air interface is

sin _c = n₂/n₁ = ^1.00/_1.33 = 0.75

_c = 48.6°

Since this light comes in to the water-air interface at an angle of incidence greater than the critical angle, all of it is reflected. That is, the light undergoes total internal reflection so all of it is reflected with an angle of reflection of 53° and none of it is refracted into the air.

23.33 What is the critical angle for diamond in air? What is the critical angle for diamond in water?

The critical angle is given by

_c = sin ^{- 1}[n₂ / n₁]

The index of refraction of diamond is n₁ = 2.4.

For a diamond in air (n₂ = 1.00), then, the critical angle is

_c = sin ^{- 1}[1.00/2.4] = sin ^{- 1}[0.417]

_c = 24.6°

For a diamond in water (n₂ = 1.33), then, the critical angle is

_c = sin ^{- 1}[1.33/2.4] = sin ^{- 1}[0.554]

_c = 33.6°

23.38 A ray of light, containing only wavelengths of 490 and 660 nm, is incident on a piece of heavy flint glass at 42°. What is the angular separation of the refracted rays inside the glass?

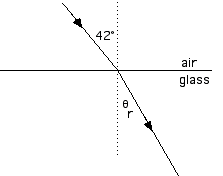
Table 23.3, on page 876, lists the index of refraction of heavy flint glass for various wavelengths; n(490 nm) = 1.664, n(660 nm) = 1.644. That means the angle of refraction qr will be different for the two wavelengths. We apply Snell’s Law for both values of the index of refraction.

n₁ sin ₁ = n₂ sin ₂

For = 490 nm and n₂ = 1.664 this becomes

(1.00) sin 42° = (1.664) sin ₂

(1.00) (0.6691) = (1.664) sin ₂

sin ₂ = 0.6691/1.664 = 0.4021

₂ = 23.71°

For = 660 nm and n₂ = 1.644 Snell’s Law gives us

(1.00) sin 42° = (1.644) sin ₂

(1.00) (0.6691) = (1.644) sin ₂

sin ₂ = 0.6691/1.644 = 0.4070

₂ = 24.02°

The difference in these two angles is 0.32°. The two colors of light are dispersed by this angle

= 0.32°

 

23.41 A ray of white light shines on an equilateral prism made of zinc crown glass so that the incoming angle of incidence equals the outgoing angle of refraction (for 590 nm light). What is the angular spread of the spectrum?

First, we must find the angle of incidence, ₁. We start with Snell’s Law,

n₁ sin ₁ = n₂ sin ₂

(1.000) sin ₁ = (1.517) sin ₂

From the symmetry of having the incoming incident angle ₁ equal to the final angle of reflection ₄, the two angles inside the glass must also be equal; ₂ = ₃. This requires that the light inside the glass be parallel to the base of the prism or that

₂ = 30°

(1.000) sin ₁ = (1.517) sin 30°

(1.000) sin ₁ = (1.517) (0.500)

sin ₁ = 0.7585

₁ = 49.33°

Now we must go back and calculate the final angle of refraction, ₄, for the extremes.

For = 430 nm (violet light), n₂ = n₃ = 1.528;

for = 770 nm (red light), n₂ = n₃ = 1.511.

We may as well start with violet light,

= 430 nm, n₂ = n₃ = 1.528

n₁ sin ₁ = n₂ sin ₂

(1.000) sin 49.33° = (1.528) sin ₂

(1.000)(0.7585) = (1.528) sin ₂

sin ₂ = ^0.7585/_1.528 = 0.496

₂ = 29.76°

We can use the geometry of a triangle -- that the sum of a triangle’s three angles is 180° -- to determine ₃,

60° + (90° - ₂) + (90° - ₃) = 180°

₃ = 60° - ₂

₃ = 60° - 29.76°

₃ = 30.24°

Again, for this glass to air interface, apply Snell’s Law,

n₄ sin ₄ = n₃ sin ₃

(1.00) sin ₄ = (1.528) sin 30.24°

sin ₄ = (1.528) (0.5036) = 0.769

₄ = 50.31°, for violet light.

Now we go through the same calculations but, this time,

for red light, = 770 nm, n₂ = n₃ = 1.511

n₁ sin ₁ = n₂ sin ₂

(1.000) sin 49.33° = (1.511) sin ₂

(1.000)(0.7585) = (1.511) sin ₂

sin ₂ = ^0.7585/_1.511 = 0.502

₂ = 30.13°

We can use the geometry of a triangle -- that the sum of a triangle’s three angles is 180° -- to determine ₃,

60° + (90° - ₂) + (90° - ₃) = 180°

₃ = 60° - ₂

₃ = 60° - 30.13°

₃ = 29.87°

Again, for this glass to air interface, apply Snell’s Law,

n₄ sin ₄ = n₃ sin ₃

(1.00) sin ₄ = (1.511) sin 29.87°

sin ₄ = (1.511) (0.4980) = 0.7525

₄ = 48.81°, for red light.

The entire spectrum of colors, then, will be spread out between the violet and red extremes,

= 50.31° - 48.81°

= 1.50°

 

23.43 Through what angle should an analyzer be rotated from the incoming plane of polarization to reduce the intensity to one-fourth?

The intensity is given by

S = S_o cos²

[This is contained in the text, on page 885, before Example 23.8; the equation given in Example 23.8, at the top of page 886, is NOT correct].

S = S_o cos²

S = S_o cos² = So/4

cos² = 0.25

cos = 0.50

= 60°

That is, cos (60°) = 0.5

23.45 [Oops, this is essentially a repeat of the previous problem; sorry about that]. Light coming from a polarizer passes through another polarizer, used as an analyzer, that has been rotated 30°. What is the intensity of the exiting light (compared to the intensity arriving at the analyzer)?

The intensity is given by

S = S_o cos²

S = S_o cos² 30° = S_o (0.866)² = S_o (0.75)

S = 0.75 S_o

23.52 What should be the initial angle of incidence onto an equilateral prism so that it equals the final angle of refraction? The index of refraction of the prism is 1.45.

This is essentially the same as problem 23.41 with a different index of refraction.

 

We must find the angle of incidence, ₁. We start with Snell’s Law,

n₁ sin ₁ = n₂ sin ₂

(1.000) sin ₁ = (1.45) sin ₂

From the symmetry of having the incoming incident angle 1 equal to the final angle of reflection ₃, the two angles inside the glass must also be equal; ₂ = ₃. This requires that the light inside the glass be parallel to the base of the prism or that

₂ = 30°

(1.000) sin ₁ = (1.45) sin 30°

(1.000) sin ₁ = (1.45) (0.500)

sin ₁ = 0.725

₁ = 46.47° 

Summary			Ch 24, Mirrors and Lenses
	Return to Ch 23 Home Page (ToC)

(c) Doug Davis, 2003; all rights reserved