Homework

Chapter 22: Alternating Current

Ch 22: 7, 11, 21, 31, 37, 46, 53

 

22.7 An electric light, connected to an ordinary 120 V AC wall outlet, uses 60 W of power. What are

a) the rms current through the light,

b) the resistance of the light, and

c) the maximum and minimum instantaneous values of the power and of the current?

P = IV

60 W = (I) (120 V)

I_rms = 0.5 A

, or

i = I(t) = I_max cos 2 f t = I_max cos 120 t

I_rms = 0.5 A

I_max = (1.414) (0.50 A)

I_max = 0.707 A

I_min = 0

Likewise,

V = V_rms = 120 V

V_max = (1.414) (120 V) = 170 V

V_min = 0

P = I V

P_max = I_max V_max = (0.707 A)(170 V)

P_max = 120 W

P_min = 0

 

22.11 A laboratory power supply provides AC electricity with a peak voltage of 27.0 volts. What is the rms voltage?

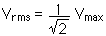
V_rms = 19.1 V

 

22.21 If 0.8 ampere flows through a capacitor when it is connected across a 120-volt, 60 Hz AC voltage source, what is the capacitance of the capacitor?

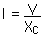
X_c = 120 V / 0.8 A = 150

C = 1.77 x 10 ^{- 5} F

C = 17.7 x 10 ^{- 6} F = 17.7 F

 

22.31 If 0.20 ampere flows through a L = 200 mH (millihenry) inductor when connected across a 30-volt AC voltage source, what is the frequency of the source?

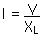
X_L = 2 f L

150 = 2 f (200 mH)

f = 150 / [2 (200 x 10 ^{- 3} H)]

f = 119 Hz

 

22.37 [Note the change in the values of the capacitor and the frequency -- and the change in the order of the calculations or questions asked!]

Consider a series RCL circuit with R = 80 , C = 15 F, L = 250 mH connected to a 12 V, 120 Hz AC source.

a) Calculate the reactances X_C and X_L.

b) What is the total impedance?

c) What current flows through the circuit?

d) What are the three potential differences across the three elements (V_R, V_C, and V_L)?

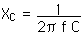
X_C = 88

X_L = 2 f L

X_L = 2 (120 s ^{- 1}) (0.250 H) = 188

X_L = 188

Z = 128

I = 0.094 A

---

The voltages we calculate across the circuit elements, like the 12 volts of the power supply itself, are all rms-values.

V_R = I R = (0.094 A)(80 ) = 7.52 V

V_C = I X_C = (0.094 A)(88 ) = 8.27 V

V_L = I X_L = (0.094 A)(188 ) = 17.67 V

Some explanation or discussion of V_C and, especially, V_L seems like it might be useful. The voltages across the capacitor and the inductor are out of phase with each other so the net voltage across the two of them is

V_net = | V_L - V_C | = | 17.67 V - 8.27 V | = 9.4 V

 

22.46 [Note the change in the value of the inductance!]

An 80 resistor in connected in series with a 50 F capacitor and a 30 mH inductor across a 120 V, 60 Hz AC voltage source.

What is the impedance of the circuit?

How much current flows in the circuit?

What is the power factor (cos ) of the circuit?

How much power is used by the circuit?

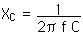
X_C = 53

X_L = 2 Ó f L

X_L = 2 (60 s ^{- 1})(0.030 H) = 11.3

X_L = 11.3

Z = 90.2

I = 1.33 A

P = I² Z cos = I V cos

cos = power factor

cos = 0.887

P = (1.33 A) (120 V) (0.887) = 141.5 W

P = 141.5 W

 

22.53 What is the resonance frequency of a series RCL circuit with a 150 resistor, a 25 F capacitor, and a 80 mH inductor? What current will flow in the circuit if it is connected to a 20 V supply at this resonance frequency? What current will flow if the frequency is increased or decreased by 20%?

At resonance Z = minimum or Z = R, so

X_C = X_L

f = 112 Hz

At this resonance frequency of 112 Hz, the total impedance is at its minimum,

Z_min = R = 150

so the current through the circuit is

At resonance, the current is 0.133 A

I_res = 0.133 A

Now increase the frequency by 20%

f₊ = (1.20) f_res = (1.20) (112 Hz) = 134 Hz

X_C = 47.5

X_L = 2 f L = 2 (134 Hz) (80 x 10 ^{- 3} H)

X_L = 67.4

Z = 151.3

Now, decrease the frequency by 20%,

f _- = (0.80) f_res = (0.80) (112 Hz) = 89.6 Hz

X_C = 71.5

X_L = 2 f L = 2 (89.6 Hz) (80 x 10 ^{- 3} H)

X_L = 45.0

Z = 152.3

And we see there is very little change in the current when the frequency is changed by 20%.

It is interesting and fun to re-do this set of calculations for R = 15 (Remember, for the case we have just looked at, we had R = 150 ). This new circuit has a much smaller resistance R.

The resonance frequency remains the same, of course. The values of the reactances, X_L and X_C, remain the same. Only R has changed. At resonance, the new resonance current is now

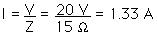
I_res = 1.33 A

 

For the higher frequency, f₊ = 134 Hz, we still have

X_C = 47.5 and X_L = 67.4

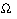
Z = 24.9

Now, decrease the frequency by 20% again, so that f _-  = 89.6 Hz, and we still have

X_C = 71.5 and X_L = 45.0

Z = 30.4

Now -- with a smaller value of the resistance R -- a variation in the frequency of 20% does, indeed, make a very large difference in the current.

Summary			Ch 23, Reflection and Refraction (Optics)
	Return to Ch 22 Home Page (ToC)

(c) Doug Davis, 2003; all rights reserved