Homework Chapter 21: Electromagnetic Induction
Ch 21: 3, 7, 19, 24, 30, 40, 48, 57, 68, 69, 78
21.3 In a region where the magnetic field is 0.02 T, what can be the maximum magnetic flux through a 20 cm x 30 cm rectangular coil? What can be the minimum flux? What makes the difference?
= A B cos
The orientation of the coil and the magnetic field make the difference:
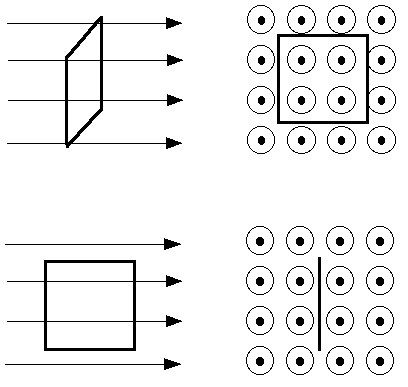
21.7 A rectangular loop has dimensions of 2.0 cm by 3.0 cm and is initially between the poles of a large magnet, where the magnetic field strength is B = 0.050 T. The loop is oriented so the normal to the plane of the coil lies parallel to the direction of the magnetic field. The coil is removed from that region to a region with no magnetic field in 0.15 seconds. What is the average induced emf?
21.19 The loop in Figure 21.30 has a radius r of 4.42 cm. The magnetic field strength is uniform and has a value of 33.0 mT. The angle between the field and a line normal to the plane of the loop is 53°.
a) Determine the magnetic flux through the loop.
b) When the magnetic field is initially turned on, the magnetic field strength rises to the value given above in 10.5 ms. What average voltage is induced in the coil?
c) If the resistance of the coil is 27.3
, what average current is induced in the coil?
Figure 21.30 Problem 21.19
A =
r2 =
= 0.012 V
I = V/R
I = 0.012 V / 27.3
I = 0.000 43 A
I = 0.43 mA
21.24 The bar magnet in Figure 21.32 is held above a loop of wire that lies in a horizontal planand then is dropped toward the loop. Find the direction of the current through the loop
a) as the magnet approaches the loop.
b) as the magnet actually passes through the loop.
c) after the magnet has passed through the loop and moves away from it.
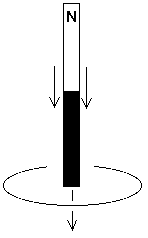
Figure 21.32 Problem 21.24
The direction of the magnetic field is from the N-pole to the S-pole (the N and S are not visible in the figure in my copy of the book&emdash;and probably not in any of the books).
a) As the magnet approaches, the loop goes from initially having no magnetic flux to having a flux with magnetic field pointing up. Therefore, the induced magnetic field (the one caused by the induced current in the loop) must point down. To get such a magnetic field, the induced current must be clockwise (or from right to left in the front part of the coil).
b) While the magnet falls through the loop, there will be no change in the flux so the current will drop to zero.
c) As the magnet leaves, the loop goes from having a flux with magnetic field pointing to having no flux. Therefore, the induced magnetic field (the one caused by the induced current in the loop) must point up (think of the induced current or induced flux as trying to restore what was previously there). To get such a magnetic field, the induced current must be counterclockwise (or from left to right in the front part of the coil.
21.30 In Figure 21.38, a loop of wire is perpendicular to a magnetic field initially pointing up (or out) with a field strength of 0.056 T. In a period of 3.5 seconds, the magnetic field decreases to zero and then increases in the opposite direction until it has a field strength of 0.034 T, pointing into the page (or down). This is illustrated in the diagram below. The area of the loop is 0.01 m2.
a) What is the induced emf in the coil?
b) The coil has a resistance of 7.8
c) In which direction does the current flow? Clockwise or counterclockwise?
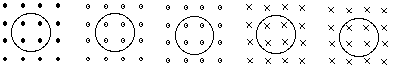
Figure 21.38 Problem 21.30
t = 0.000 90 W / 3.5 s
V
I = V/R = (0.000 26 V)/(7.8
I = 0.033 mA
Initially, the magnetic field is strong and pointing out of the page (or screen). As it decreases, the induced magnetic field will try to increase it. To have an induced magnetic field pointing out of the page (or screen), the induced current must be counter-clockwise as shown in the sketch here.
21.40 What is the maximum potential difference of a simple generator made of a square coil 10.0 cm on each side with 200 turns of wire and rotating at 60.0 rev/s in a 0.500 T magnetic field?
t
f =
or
A note of caution: BE SURE to use "consistent units". While it is easier to say and think A = (10 cm)2 = 100 cm2, all the dimensions must be in meters. That is, A = (0.10 m)2 = 0.01 m2.
21.48 Find the inductance of a coil if an average emf of 100 mV is produced when the current changes from 0 to 1.5 A is 0.30 s.
100 mV = 0.100 V = - L [ - 1.5 A / 0.30 s]
0.100 V = - L [- 5]
L = 0.100 / 5
L = 0.02 H = 20 mH
21.57 Consider a series RL circuit consisting of a 30 mH inductor, 6.0
The switch is closed at t = 0. Find the following:
a) the time constant of the circuit.
b) the current long after the switch is closed.
c) the current after one time constant
L = 30 mH = 0.030 H
= L / R = [0.030 / 6] = 0.005 = 0.005 s
If = V/R = 12 V / 6
i = i(t) = If [ 1 - e - t /
i( t=
i( t=
i( t=
i( t=
21.68 An electric motor has a resistance of 3.5
Vnet = I R = (4.5 A) (3.5 Vnet = V -
21.69 An automobile starter motor draws 3.5 A from a 12 V battery when operating at normal speed. A broken pulley locks the motor in position and the current increases to 18 A. What is the back emf?
When is is locked, there is no back emf. From the information about the motor when it is locked, we can find its resistance R,
R = V / I = 12 V / 18 A = 0.67 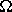When the starter motor is running, the net voltage is (far) less than 12 V,
Vnet = I R = (3.5 A) (0.67 W) = 2.33 V Vnet = V -
21.78 A transformer has 630 turns in its primary and 2520 in its secondary. The input potential difference is 120 V and the input current is 8.00 A. What are the output potential difference and current?
V2 / N2 = V1 / N1 V2 = V1 [ N2 / N1]
V2 = [120 V] [ 2520 / 630 ]
V2 = [120 V] [ 4 ]
V2 = 480 V
P2 = P1
P2 = I2 V2 = I1 V1 = P1
I2 V2 = I1 V1
I2 = I1 [ V1 / V2]
I2 = [8 A] [120 V / 480 V]
I2 = 2.0 A
(c) Doug Davis, 2003; all rights reserved
Return to Ch 21 Home Page (ToC)
