Homework

Chapter 20: Magnetism

Ch 20: 4, 12, 21, 24, 30, 64

 

20.4 A charge of 1.5 x 10 ^{- 10} C moves at 1.0 km/s through a magnetic field in such a direction that the magnetic force on it is a maximum. What is the magnetic field strength if the maximum force on the charge is 8 x 10 ^{- 8} N?

F = q v B sin

F_max = q v B

B = F_max/[q v]

B = 8 x 10 ^{- 8} N / [(1.5 x 10 ^{- 10} C)(1 000 m/s)]

B = 0.533 T

 

20.12 An electron moves in a circular path, perpendicular to a magnetic field of B = 1.25 T, with a a speed of 1.2 x 10⁴ m/s. What is the radius of the electron's circular path?

F_mag = q v B sin

Since = 90, sin = 1

F_mag = q v B

This is also the centripetal force,

F_c = m v² / r

q v B = m v² / r

r = m v / [q B]

r = (9.11x10^-31 kg) (1.2x10⁴ m/s) / [(1.6x10^-19 C) (1.25 T)]

r = 5.47 x 10^-8 m

 

20.21 A 100 T magnetic field is confined to a 5.0-cm region as shown in Figure 20.47. An electron passes through the region with a speed of 5.16 x 10⁶ m/s as shown. Determine the angular deflection .

[ The 100 T magnetic field is so very strong that it does not just deflect the electron a little like my analysis assumes. Rather, the electron would make a circle -- or half a circle. So the numbers are unrealistic! Try two variations of this:

20.21 a; An electron enters a region where the magnetic field is 100 T, moving perpendicular to the magnetic field with a speed of 5.16 x 10⁶ m/s. What is the radius of the circle that it now moves it? It will make a half circle "orbit" and then exit the region with the magnetic field. What is the radius of that semicircular path.

 

20.21 b; Earth's magnetic field is about 5 x 10 ^{- 5} T or 50 x 10 ^{- 6} T. A somewhat larger magnetic field of 100 x 10 ^{- 6} T is confined to a 5.0-cm region as shown in Figure 20.47. An electron passes through the region with a speed of 5.16 x 10⁶ m/s as shown. Determine the angular deflection .

This second question is the one whose solution I had initially.]

---

20.21 a; An electron enters a region where the magnetic field is 100 T, moving perpendicular to the magnetic field with a speed of 5.16 x 10⁶ m/s. What is the radius of the circle that it now moves it? It will make a half circle "orbit" and then exit the region with the magnetic field. What is the radius of that semicircular path.

With the magnetic field this strong, the electron is not going to be deflected just a little. It is going to move in a circle -- actually in a semi-circle. The magnetic force is

F_mag = q v B

F_mag = (1.6 x 10 ^{- 19} C)(5.16 x 10⁶ m/s)(100 T)

F_mag = 8.26 x 10 ^{- 11} N

This force provides the centripetal force,

F_c = m v²/r

r = m v²/F_c

r = (9.11 x 10 ^{- 31})(5.16 x 10⁶ m/s)² / (8.26 x 10 ^{- 11} N)

r = 2.9 x 10 ^{- 7} m

That's a very small radius -- but the mass of the electron is very small, too

---

20.21 b; Earth's magnetic field is about 5 x 10 ^{- 5} T or 50 x 10 ^{- 6} T. A somewhat larger magnetic field of 100 x 10 ^{- 6} T is confined to a 5.0-cm region as shown in Figure 20.47. An electron passes through the region with a speed of 5.16 x 10⁶ m/s as shown. Determine the angular deflection .

This second question is the one whose solution I had initially.]

 

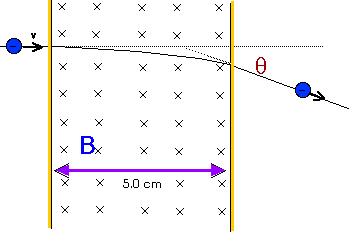
Figure 20.47 Problem 20.21

20.21b assumes that v_x remains constant. Then we can use that to determine the time the electron spends with this magnetic force on it. That will let us calculate v_y and, from that, the deflection angle.

First, find the force on the electron,

F = q v B sin

Since = 90, sin = 1.0

F = (1.6 x 10 ^{- 19} C) (5.16 x 10⁶ m/s) (100 x 10 ^{- 6} T) (1.0)

F = 8.256 x 10 ^{- 17} N

While this seems like a very small force, remember it is acting on a very small mass, the mass of the electron,

F = m a

a = F / m

a = 8.256 x 10 ^{- 17} N / 9.11 x 10 ^{- 31} kg

a = 9.16 x 10¹³ m/s²

How long does this acceleration act?

v = s/t

t = s/v

t = 0.05 m / ( 5.16 x 10⁶ m/s )

t = 9.69 x 10 ^{- 9} s

If that acceleration is all in the y-direction, what will be the final velocity component in the y-direction?

v_y = v_yo + a_y t

v_y = 0 + (9.16 x 10¹³ m/s²) (9.69 x 10^-9 s)

v_y = 8.88 x 10⁵ m/s

The deflection angle is given by

tan = v_y / v_x

If we use the approximation that v_x = v_xo = 5.16 x 10⁶ m/s, then

tan = (8.88 x 10⁵ m/s) / (5.16 x 10⁶ m/s)

tan = 0.172

= 9.76^o

With such a small deflection angle, our two approximations are, indeed, reasonable. The acceleration is almost entirely in the y-direction and the x-component of the velocity remains nearly constant.

 

20.24 In a region where Earth's magnetic field is 5.0 x 10 ^{- 5} T and makes an angle of 60° with Earth's surface, determine the force on a straight 2.0 m wire that carries a current of 8.0 A straight up.

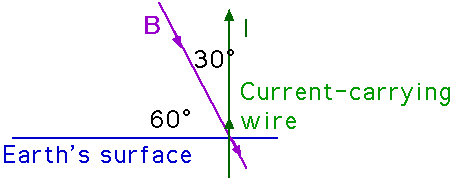
F = I l B sin

F = (8.0 A) (2.0 m)( 5.0 x 10 ^{- 5} T) (sin 30°)

F = (8.0 A) (2.0 m) (5.0 x 10 ^{- 5} T) (0.50)

F = 4 x 10 ^{- 4} N

The force is perpendicular to both the magnetic field and the current. The force is directed into the paper (or screen). Yes, it really is into the paper (or screen)!

 

20.30 An electric transmission line carries 2,500 A of current from east to west. What is the magnetic field 10 m below the line?

From Equation 20.10,

B = 5 x 10^-5 T

 

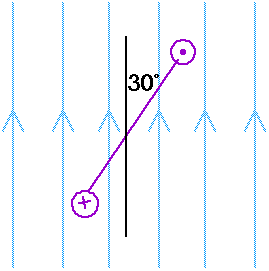
20.54 A 4.5 A current flows through a 20-turn rectangular coil of 2.5 x 10 ^{- 2} m² area. The coil is rotated in a 0.20 T magnetic field. Calculate the torque for each of the orientations shown below.

(a)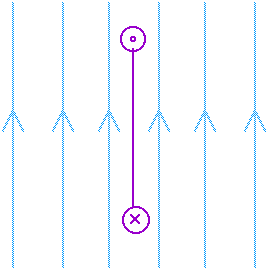

(b)

 

(c)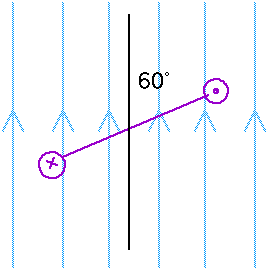

(d)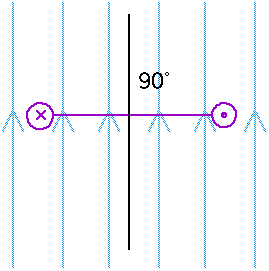

Figure 20.54 Problem 20.54.

The symbol indicates a wire carrying a current coming out of the page; indicates a current going into the page. 

= N I A B sin

= (20)(4.5 A)(0.025 m²)(0.20 T) sin

The angle in this equation is the angle between the magnetic field and the normal (the direction perpendicular) to the plane of the coil. That is, is the angle between the magnetic field and a line drawn perpendicular to the plane of the coil. This means the angles for this equation are not the angles labeled in these figures; rather is 90^o minus each of these angles! Be careful with this! 

For part (a)

= 90^o, sin = 1.00

= (20) (4.5 A) (0.025 m²) (0.20 T) (1.00)

= 0.45 m-N 

For part (b)

= 60^o, sin = 0.866

= (20) (4.5 A) (0.025 m²) (0.20 T) (0.866)

= 0.39 m-N 

For part (c)

= 30^o, sin = 0.500

= (20) (4.5 A)(0.025 m²) (0.20 T) (0.500)

= 0.225 m-N 

For part (d)

= 0^o, sin = 0

t = (20) (4.5 A) (0.025 m²) (0.20 T)(0.)

= 0

 

20.64 [ Please omit question 20.64]. A single, rectangular loop of wire, 8 cm by 12 cm, is suspended from a balance so that it is perpendicular to a magnetic field. After being balanced, a current of 1.75 A is turned on and flows through the coil. Then an additional 15.8 g must be added to the other arm of the balance to again balance the system. What is the strength of the magnetic field? 

Correction needed! A current loop experiences a torque in a magnetic field. The net force on a current loop in a magnetic field is zero! Therefore, this problem is wrong as it is actually written. Modify the problem so that the magnetic field does not extend to the top of the loop but does extend beyond the bottom of it.

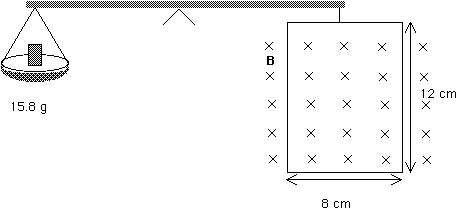
Figure 20.57 Problem 20.64

With the modification that the magnetic field does not extend to the top wire but does extend beyond the bottom wire, this problem becomes one of finding the magnetic field that causes a force of

w = m g = (0.0158 kg)(9.8 m/s²) = 0.155 N

on the bottom wire

F = I l B sin  

For our present geometry, with the field perpendicular to the plane of the loop, = 90° or sin = 1.0

F = I l B

B = F / I l

B = 0.155 N / [ (1.75 A) (0.08 m) ]

B = 1.11 T

Summary			Ch 21, Induction
	Return to Ch 20 Home Page (ToC)

(c) Doug Davis, 2003; all rights reserved