Homework

Chapter 19:

Direct - Current Circuits

Ch 19: 5, 11, 18, 37, 46, 54, 75, 80, 83

 

19.5 A carbon resistor has a resistance of 50 when measured at room temperature. What is its resistance when immersed in liquid nitrogen which is at its boiling temperature ( - 196°C)?

R = R_o (1 + T)

Take "room temperature" to be about 25^oC.

The boiling temperature of liquid nitrogen is - 196^oC.

Therefore,

T = T_f - T_i = ( - 196^oC) - (25^oC) = - 221C^o

For carbon, the temperature coefficient , is - 0.0005 / C^o (notice the minus sign!),

R = R_o (1 + T)

R = ( 50 ) ( 1 + [ - 0.0005 / C^o ] [ - 221C^o ] )

R = ( 50 )( 1 + 0.1105 )

R = (50 )( 1.1105 )

R = 55.5

For most materials, a reduction in temperature would mean a reduction in resistance. But carbon is the exception; reducing its temperature causes an increase in resistance.

 

19.11 A resting human neuron has a potential difference of about 75 mV across it and the current through it is about 200 A. How much power is being released in the neuron?

P = I V

P = (200 x 10 ^{- 6} A)(75 x 10 ^{- 3} V)

P = 1.5 x 10 ^{- 5} A - V

Now, what is an A - V (an amp - volt)?

P = 1.5 x 10 ^{- 5} A - V

P = 1.5 x 10 ^{- 5} W

 

19.18 Ordinarily wire is specified as "10 - gauge" wire or "12 - gauge" wire and so on rather than specifying its diameter. The table below gives the correlation between gauge specification and diameter. Notice that the larger the gauge number, the smaller the wire. For each gauge of wire, calculate the resistance of a 10 - m piece of copper wire.

Gauge number	diameter
8	0.3264 cm
10	0.2588 cm
12	0.2053 cm

The resistance R is given by R = r L / A. For copper, the resistivity is r = 1.59 x 10 ^{- 8} - m. For each piece of wire, the length is L = 10 m. We need to calculate the cross - section area

A = r² = (d/2)² = d²/4

For simple and repeated calculations, I like to use a spreadsheet.

For ClarisWorks (and most spreadsheets) the notation 1.63e-3 means 1.63 x 10 ^{- 3}.

19.37 Calculate the power supplied by a 12 - volt power supply in the circuit if the resistors have the following values: R₁ = 250 , R₂ = 750 , and R₃ = 1000 . Calculate the power used by each resistor.

Figure 19.33 Problem 19.37

 

These resistors are in series so the equivalent resistor has a resistance Req given by

R_eq = R₁ + R₂ + R₃

R_eq = 250 + 750 + 1000 = 2000

The current through this equivalent resistor would be

R = V / I

I = V / R = (12 V) / (2000 ) = 0.006 A = 6 mA

This is the current supplied by the battery and the power supplied by the battery is

P = IV

P = (0.006 A)(12 V) = 0.072 W = 72 mW

P = 72 mW

Now, to find the power absorbed by each of the resistors, we could find the voltage across each of the resistors. We know the current through each of the resistors (0.006 A = 6 mA) and we know each resistance so we will use an expression for power that requires only the current and resistance,

P = I V

P = I (IR) = I² R

P₁ = (0.006 A)² (250 ) = 0.009 A² = 0.009 W

P₂ = (0.006 A)² (750 ) = 0.027 A² = 0.027 W

P₃ = (0.006 A)² (1000 ) = 0.036 A² W = 0.036 W

P_tot = P₁ + P₂ + P₃ = 0.072 W

And, of course, that is just the power supplied by the battery to the equivalent resistor.

We ought to convince ourselves that the units are correct; that is, that units of A² W are, indeed, units of watts, W.

A² W = A² (V / A) = A - V

and in problem 19.11 we already found that

A - V = W

that is, that

(amp)(volt) = watt

 

19.46 Calculate the power supplied by the 12 - volt power supply in the circuit above if the resistors have the following values: R₁ = 250 , R₂ = 750 , and R₃ = 1000 . Calculate the power used by each resistor.

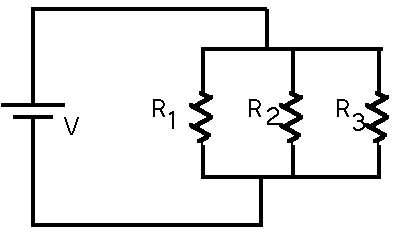
Figure 19.34 Problem 19.46

These resistors are connected in parallel so the equivalent resistance, Req, is given by

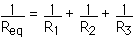
R_eq = 158

The current supplied by the battery to this equivalent resistor would be

R = V / I

I = V / R

I = 12 V / 158 = 0.076 A

The power supplied by the battery to this equivalent resistor would be

P = I V

P = (0.076 A) (12 V) = 0.912 W

P = 0.912 W

To find the power supplied to each individual resistor, we can use an expression that requires the resistance and the voltage since we know that for each resistor,

P = I V = (V/R) V = V² / R

For each resistor, V = 12 V, since they are in parallel,

P₁ = V² / R₁ = (12 V)² / 250 = 0.576 W

P₂ = V² / R₂ = (12 V)² / 750 = 0.192 W

P₃ = V² / R₃ = (12 V)² / 1000 = 0.144 W

P_tot = P₁ + P₂ + P₃ = 0.912 W

And, of course, that is just the power supplied to the equivalent resistor.

And we need to convince ourselves that we have, indeed, handled the units correctly. That is, is a watt (W) truely the same as V² / ?

V² / = V² / (V / A) = V / ( 1 / A ) = V - A = W

as we saw in problem 19.11.

 

19.54 Find the equivalent resistance in the circuit shown in Figure 19.36 for R₁ = 100 , R₂ = 500 , R₃ = 750 , R₄ = 1000 , R₅ = 50 . If these are connected to a 12 - volt battery, what is the power supplied to the equivalent resistor? Find the current through each of the individual resistors and the power supplied to each.

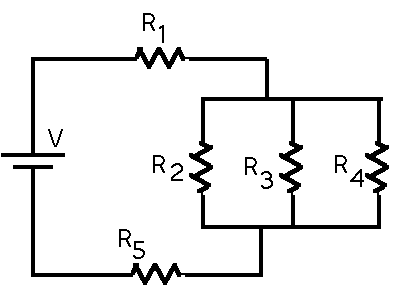
Figure 19.36 Problem 19.54

Resistors R₂, R₃, and R₄ are connected in parallel, so the first thing we will do is find the single resistor that is equivalent to just those three.

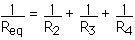
R_eq = 231

We will shortly need to calculate another equivalent resistance, so let's call this one R_eq,1. Now our circuit looks like this -

I think it is clear that these three resistors, R₁, R_eq,1, and R₅ are in series. If that is not entirely clear, it may help to redraw the circuit diagram as

For these three resistors in series, the equivalent resistance is given by

R_eq = R₁ + R_eq,1 + R₅

and to avoid confusion, we will label this one as R_eq,2; that is,

R_eq,2 = R₁ + R_eq,1 + R₅

R_eq,2 = 100 + 231 + 50

R_eq,2 = 381

That is, our equivalent single - resistor circuit would be

with R_eq,2 = 381 . The current through this circuit is

R = V / I

I = V / R

I = 12 V / 381

I = 0.0315 A

The power given out by the battery and absorbed by this single resistor is

P = I V

P = (0.0315 A) (12 V)

P = 0.378 W

This means the same current of 0.0315 A flows through each of the resistors in the previous all series circuit,

Now we can find the potential difference across R1, R5, and Req,1 and the power absorbed by each resistor.

R = V / I

V = I R

V₁ = (0.0315 A) (100 ) = 3.15 V

V₅ = (0.0315 A) (50 ) = 1.575 V

Veq,1 = (0.0315 A) (231 ) = 7.275 V

Notice that V₁ + V_eq,1 + V₅ equals the 12.0 volts of the battery.

Knowing the current through each of these resistors and the voltage across each, it is now easy to calculate the power used by each,

P = I V

P₁ = I V₁ = (0.0315 A) (3.15 V) = 0.0992 W

P₅ = I V₅ = (0.0315 A) (1.575 V) = 0.0496 W

P_eq,1 = I V_eq,1 = (0.0315 A) (7.275 V) = 0.2292 W

As an intermediat check, notice that

P₁ + P_eq,1 + P₅ = 0.378 W

which is the power supplied to the single equivalent resistor R_eq,2. That is as it ought to be, of course.

Each of the resistors R₂, R₃, and R₄ in the bank of parallel resistors has a voltage of 7.275 V across it so the current through each is given by

R = V / I

I = V / R

I₂ = 7.275 V / 500 = 0.01455 A

I₃ = 7.275 V / 750 = 0.0097 A

I₄ = 7.275 V / 1000 = 0.007275 A

Notice, again, that the sum of these currents,

I₂ + I₃ + I₄ = 0.0315 A

is the current through resistors R₁ and R₅ with which this group are in series.

The power supplied to each of these resistors is

P = I V

P₂ = I₂ V = (0.01455 A) (7.275 V) = 0.1058 W

P₃ = I₃ V = (0.0097 A) (7.275 V) = 0.0706 W

P₄ = I₄ V = (0.007275 A) (7.275 V) = 0.0529 W

As a final check, look at the power supplied to each individual resistor,

P_tot = P₁ + P₂ + P₃ + P₄ + P₅

P_tot = 0.0992 W + 0.1058 W + 0.0706 W +

+ 0.0529 W + 0.0496 W = 0.3781 W

P_tot = 0.378 W

And that is the power supplied by the battery to the single equivalent resistor that we calculated long ago.

 

19.75 A 12.0 V automobile battery (ie, a battery with an emf of 12.0 V) has an internal resistance of 0.15 . The equivalent resistance of the headlights on the automobile is 6 . Find the terminal voltage of the battery when the headlights are turned on. The resistance of the starter motor is only 0.1 . Find the terminal voltage of the battery when the starter is also turned on.

A good circuit diagram will be very helpful.

When only the lights are on, the external resistance is R = 6.0 . The total equivalent resistance of the entire circuit - including the internal resistance of the battery - then is

R_tot = R_int + R

R_tot = 0.15 + 6.0 = 6.15

From this we can find the current through the circuit,

I = V / R

I = 12 V / 6.15 = 1.951 A

This causes a drop in the terminal voltage due to the internal resistance of

V_int = I R_int = (1.951 A)(0.15 )

V_int = 0.293 V

Therefore the terminal voltage will be

V_trm = E - V_int

V_trm = 12.0 V - 0.293 V

V_trm = 11.7 V

As you can see, there is some small change in the voltage - but not very much. However, if we try to start the car, now we will notice a large effect.

When we try to start the car the starter motor (R₁ = 0.10 ) and the lights (R₂ = 6.0 ) are connected in parallel. Their equivalent resistance is given by

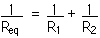
R_eq = 0.098

Notice that this is very nearly the resistance of the starter motor. The fact that the lights are also on has very little effect on the circuit. Now we go through exactly the same reasoning and calculations as before - but contrast the results!

The total equivalent resistance of the entire circuit - including the internal resistance of the battery - now is

R_tot = R_int + R

R_tot = 0.15 + 0.098 = 0.248

From this we can find the current through the circuit,

I = V / R

I = 12 V / 0.248 = 48.32 A

(This is a very large current! The wire which carries this current goes directly from the battery to the starter and is very thick; look for it sometime). This causes a drop in the terminal voltage due to the internal resistance of

V_int = I R_int = (48.32 A)(0.15 )

V_int = 7.25 V

Therefore the terminal voltage will be

V_trm = E - V_int

V_trm = 12.0 V - 7.25 V

V_trm = 4.75 V

Now the terminal voltage is less than half what it was before! You will clearly see the lights dim!

 

19.80 For a series RC circuit with R = 1.5 k, C = 25 F, and V_bat = 18 V, find the following:

a) the initial current.

b) the final charge on the capacitor.

c) the time constant of the circuit.

d) the current and capacitor charge after two time constants.

e) the time at which the current has dropped to one - half of its initial value.

Let's begin with a circuit diagram -

a) the initial current.

Always, the current is just the net voltage divided by the resistance,

Initially, before there is any charge on the capacitor, the cnet voltage is just the voltage of the battery. Therefore, initially, before there is any charge on the capacitor, the current is just this net voltage, the voltage of the battery, divided by the resistance,

I_o = V / R = 18 V / 15,000

I_o = 0.0012 A = 1.2 mA

b) the final charge on the capacitor.

Finally, when there is no more current, the potential difference across the capacitor will be the same as the potential difference across the battery (18 V). This means the net voltage is zero so the current is zero.

What charge must this capacitor have to have a voltage of 18 V?

C = Q / V

Q = C V

Q_f = (25 x 10 ^{- 6} F) (18 V)

Q_f = 0.000 45 C = 0.45 mC = 450 C

c) the time constant of the circuit.

The time constant is given by

= RC

= (1 500 W) ( 25 x 10 ^{- 6} F)

= 0.0375 s

d) the current and capacitor charge after two time constants.

The current, as a function of time is given by

i = I_o

For t = 2 , this is

i = (1.2 mA) e ^{- 2}

i = (1.2 mA) (0.135)

i = 0.162 mA

The charge on the capacitor, as a function of time, is

q = Q_f [ ]

For t = 2 , this is

q = [450 C] [ 1 - e ^{- 2} ]

q = [450 C] [ 1 - 0.135 ]

q = [450 C] [ 0.865 ]

q = 389 µC

e) the time at which the current has dropped to one - half of its initial value.

As we already know, the current, as a function of time is given by

i = I_o

For what time t is i = 0.5 Io?

i = 0.5 I_o = I_o

0.5 =

The "natural logrithm" (written as ln(x) or labeled on a calculater as "ln") is the inverse of the exponential function. That is,

ln(e^x) = x

ln (0.5) = - 0.693

ln () = - t /

Therefore,

- t / = - 0.693

t = 0.693

t = (0.693) (0.0375 s)

t = 0.026 s

19.83 The capacitor in the circuit sketched below is initially charged with 5 x 10 ^{- 4} C of charge. At time t = 0 the switch is closed; find the following:

a) the initial current.

b) the time constant of the circuit.

c) the time at which one - half the charge remains on the capacitor.

Initially, the potential difference across the capacitor is

V_o = C Q_o

V_o = (400 x 10 ^{- 6} F) (500 x 10 ^{- 6} C)

V_o = 2 x 10 ^{- 7} V

This means the initial current will be

I = V / R

I_o = V_o / R

I_o = (2 x 10 ^{- 7} V) / (150 )

I_o = 3 x 10 ^{- 5} A = 30 A

The time constant of this circuit is

= R C

= (150 ) (400 x 10 ^{- 6} F)

= 0.02 s

The charge on the capacitor, as a function of time, is

q = Q_o

For what value of time t is q = 0.5 Q_o?

q = 0.5 Q_o = Q_o

0.5 =

ln(0.5) = ln( )

- 0.693 = - t /

t = 0.693

t = (0.693) (0.02 s)

t = 0.0139 s

Summary			Ch 20, Magnetism
	Return to Ch 19 Home Page (ToC)

(c) Doug Davis, 2002; all rights reserved