Homework

Chapter 18: Electric Potential & Capacitance

Ch 18: 1, 3, 10, 11, 21, 23, 27, 40, 59, 64, 68

 

18.1 What is the potential difference between two points if 6 J of work is required to move 12 C of charge from one point to the other?

PE_el = W = 6 J

V = 0.5 V

 

18.3 The electric field in the region between two parallel plates connected to a 12-volt power supply is 100 N/C. What is the separation distance between the plates?

We can use Equation 18.10,

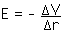
r = 0.12 m = 12 cm

The minus sign just says the potential increases in the direction opposite to the electric field.

 

18.10 Electrons in a color television are accelerated through a potential difference of about 25,000 V. With what speed do they strike the front of the picture tube? 

KE = PE = V q = V e

KE = (¹/₂) m v² = (25,000 V) (e) = 25,000 eV = 25 keV

(¹/₂) (9.11 x 10-31 kg) v² = 25,000 eV

v² = 8.78 x 10¹⁵ m²/s²

v = 9.37 x 10⁷ m/s

That is nearly one-third the speed of light!

  

18.21 How many electrons, accelerated through a potential difference of 20,000 V, must bombard one gram of water to raise its temperature 1.0 C°?

First, how much energy, in joules, does each single electron have?

E = 20,000 eV

E = 3.2 x 10^-15 J

Now, how much energy is required to raise the temperature of one gram of water by T = 1 C°? That requires ideas about specific heat from Chapter 12 from last semester. In particular, we need Equation 12.5, 

Q = c m T 

For water, the specific heat, c, is

c = 4186 J/kg C^o

Q = (4186 J/kg C^o) (0.001 kg) (1.0 C^o) = 4.186 J

How many electrons, each with energy of E = 3.2 x 10 ^{- 15} J, must deposit their energy into the water to give it 4.186 J of energy?

Q = 4.186 J = n E = n (3.2 x 10 ^{- 15} J)

n = 1.31 x 10¹⁵ electrons

  

18.23 The electric potential values at four pointson the perimeter of a square are as given in Figure 18.43. The square measures 0.10 m on a side and each point is in the center of a side. Find the magnitude and direction of the electric field at the center.

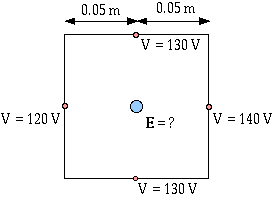
Figure 18.43 Problem 18.23

For a uniform electric field we have written

where the distance r is parallel to the electric field E. And it is also true that we can write the components of the electric field as

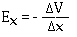
and

For the values of V given in the diagram, there is no change in the electric potential as we move vertically -- along the y-direction. This means

E_y = 0

When we move from one side of the square to the other horizontally -- in the x-direction -- there is a change in potential of

V = 140 V - 120 V

V = 20 V

This change in electric potential occurs over a change of horizontal distance of

x = 0.10 m

E_x = - 200 N/C

Since

E_y= 0

this means

E = 200 N/C

and the direction of the electric field points to the left. That means the electric field points toward lower electric potential. Think of which direction a positive test charge would move.

 

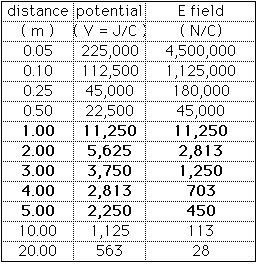
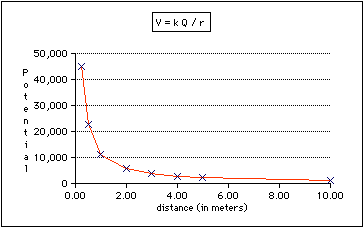
18.27 What is the electric potential at a distance of 1.00, 2.00, 3.00, 4.00, and 5.00 m from a 1.25 µC charge? What is the electric field at each of those distances? Make graphs of electric potential versus distance and of electric field strength versus distance. 

The potential is calculated from

V = k Q / r

and the electric field is calculated from

E = k Q / r²

These calculations can be done readily by a spreadsheet

For Q = 1.25 C = 1.25 x 10 ^{- 6} C = 0.000 001 25 C, this gives

  

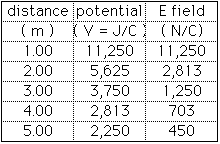
Before we make the graph, let us do a few more calculations at some more distances, just to make the graph smoother and, perhpas, more interesting or informative,

  

While you can certainly make nicer graphs by hand or by using Graphical Analysis, we can also let ClarisWorks make these graphs for us,

 

  

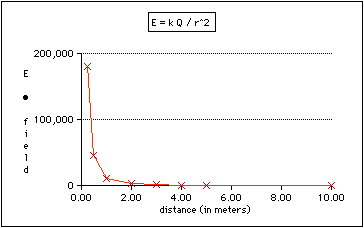
18.34 What is the electric potential at the unfilled corner of the square in the figure below?

Figure 18.45 Problem 18.34

Calculate the potential due to each individual charge and then add those together for the net potential. Potential is a scalar so this will be ordinary, common, scalar addition

V = k Q / r

V₂ = (9 x 10⁹) ( - 2 x 10 ^{- 6}) / 1.0 = - 1.8 x 10⁴ V

V₃ = (9 x 10⁹) ( + 3 x 10 ^{- 6}) / 1.414 = + 1.35 x 10⁴ V

V4 = (9 x 10⁹) ( - 4 x 10^-6) / 1.0 = - 3.6 x 10⁴ V

V_net = V₂ + V₃ + V₄ = - 4.05 x 10⁴ V

V_net = - 4.05 x 10⁴ V

 

18.40 A 120 F capacitor stores ± 180 C of charge on its plates. What is the voltage of the battery to which it is connected?

C = Q/V

or

V = Q/C

V = 180 C / 120 F

V = 1.5 V

 

18.59 To run a particular laser, 9.5 J of energy must be discharged through a "flashlamp" to provide an intense flash of light. This energy is released by a capacitor that has been charged by a 12 kV power supply. What is the capacitance of this capacitor? How much charge is stored and then released?

PE_cap = Q V / 2

Q = 2 PE_cap / V

Q = (2) (9.5 J) / 12,000 V = 1.58 x 10 ^{- 3} C

Q = 1.58 x 10 ^{- 3} C

is the charge stored and then released by the capacitor. 

C = Q / V

C = 1.58 x 10 ^{- 3} C / 12,000 V = 1.32 x 10 ^{- 7} F

C = 0.132 F

 

18.64 In the series capacitor circuit shown below C₁ = 1.0 F, C₂ = 2.5 F, C₃ = 5.0 F, and V = 12.2 V. Find the equivalent capacitance of this circuit. What energy is stored in the equivalent capacitor? Calculate the voltage across each of the capacitors and the energy stored in each capacitor.

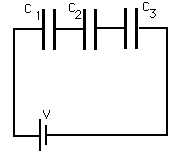
Figure 18.47 Problem 18.67

The equivalent capacitance is given by

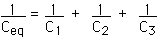
C_eq = 0.625 F

PE_cap = C (V)² / 2 = (0.625 x 10 ^{- 6}) (12.2)² / 2

PE_cap = 4.65 x 10 ^{- 5} J

This is the energy that would be stored in the single equivalent capacitor or the total energy stored in the three individual capacitors. 

Now we must find the voltage across each individual capacitor and the energy stored in each individual capacitor. The charge on each capacitor is the same and is the same as the charge on the equivalent capacitor,

C = Q/V or V = Q/C or Q = C V

Q = C V = (0.625 x 10 ^{- 6}) (12.2) = 7.625 x 10 ^{- 6} C

V1 = Q/C₁ = 7.625 x 10 ^{- 6} C / 1.00 x 10 ^{- 6} F = 7.625 V = V₁

V2 = Q/C₂ = 7.625 x 10 ^{- 6} C / 2.50 x 10 ^{- 6} F = 3.05 V = V₂

V3 = Q/C₃ = 7.625 x 10 ^{- 6} C / 5.00 x 10 ^{- 6} F = 1.525 V = V₃

V_tot = V₁ + V₂ + V₃ = 12.2 V 

Now, for the energy in each capacitor,

PE_cap = Q² / 2C

PE_cap,1 = Q²/2C₁ = (7.625 x10 ^{- 6} C)²/[2(1.00 x 10 ^{- 6} F)] = 2.91 x 10 ^{- 5} J

PE_cap,2 = Q²/2C₂ = (7.625 x 10 ^{- 6} C)²/[2(2.50 x 10 ^{- 6} F)] = 1.17 x 10 ^{- 5} J

PE_cap,3 = Q²/2C₃ = (7.625 x 10 ^{- 6} C)²/[2(5.00 x 10 ^{- 6} F)] = 5.81 x 10 ^{- 5} J

PE_cap,tot = PE_cap,1 + PE_cap,2 + PE_cap,3 = 4.65 x 10 ^{- 5} J 

And, as we would expect -- as we must have -- this is the energy stored in the equivalent capacitor. Note, too, that the powers of ten now match as well!

  

18.68 Find the equivalent capacitor for the following circuit. Determine the energy stored in this equivalent capacitor. Find the voltage across each of the individual capacitors and the charge and energy stored in each.

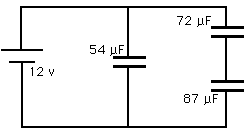
Figure 18.49 Problem 18.68

First, find an equivalent capacitor for the two that are in series,

For series capacitors, the equivalent capacitor is given by

Now we can re-draw this circuit as

and find the new equivalent capacitor that replaces the 54 F capacitor and the 39 F capacitor which are now connected in parallel. For such parallel capacitors, the equivalent capacitor is given by

C_eq = C₁ + C₂

C_eq = 54 F + 39 F = 93 F

C_eq = 93 F

The energy stored in this equivalent capacitor is

PE_cap = C(V)² / 2

PE_cap = (93 x 10^-6) (12)² / 2

PE_cap = 6.7 x 10^-3 J = 6.7 mJ

PE_cap = 6.7 mJ

Now, what is happening to each of the individual capacitors?

54 F: The voltage across this capacitor is the full 12 V

Q = C V = ( 54 x 10 ^{- 6} ) (12) = 6.48 x 10 ^{- 4} C

PE_cap = C (V)² / 2 = ( 54 x 10 ^{- 6} ) (12)² / 2 = 3.89 x 10 ^{- 3} J 

72 F and 87 F capacitors in series: Their equivalent capacitor of 39 x 10^-6 F or 39 F has 12 V across its ends so the charge on that equivalent capacitor is

Q = C V = ( 39 x 10 ^{- 6} ) (12) = 4.68 x 10 ^{- 4} C

and this is also the charge on the 72 F capacitor and the charge on the 87 F capacitor since they are in series 

72 F: The voltage is given by

V = Q / C = 4.68 x 10 ^{- 4} / 72 x 10 ^{- 6} = 6.5 V

The charge is 4.68 x 10 ^{- 4} C since that is the same as the charge on the equivalent capacitor.

The energy stored in the capacitor is

PE_cap = C (V)² / 2 = ( 72 x 10 ^{- 6} ) ( 6.5 )² / 2 = 1.51 x 10 ^{- 3} J 

87 F: The voltage is given by

V = Q / C = 4.68 x 10 ^{- 4} / 87 x 10 ^{- 6} = 5.4 V

Notice that 6.5 V + 5.4 V = 11.9 V ­ 12.0 V. This is due to rounding error since the equivalent capacitor was really 39.396 F which we wrote as merely 39 F. If we want greater accuracy, we can keep all the results to one or two more significant figures.

The charge stored in this capacitor is 4.68 x 10^-4 C since that is the same as the charge on the equivalent capacitor.

The energy stored in the capacitor is

PE_cap = C (V)² / 2 = ( 87 x 10 ^{- 6} ) (5.4)² / 2 = 1.27 x 10 ^{- 3} J 

The energy stored in these two capacitors is

PE = 1.51 x 10 ^{- 3} J + 1.27 x 10 ^{- 3} J = 2.78 x 10 ^{- 3} J

and that should be very close to the energy stored in this equivalent capacitor

PE_cap = C (V)² / 2 = ( 39 x 10 ^{- 6} ) (12)² / 2 = 2.80 x 10 ^{- 3} J

Again, the small discrepency is simply a rounding error

Summary			Ch 19, Direct Current Circuits
	Return to Ch 18 Home Page (ToC)

(c) Doug Davis, 2002; all rights reserved