PHY 1150
Chapter 15; Periodic Motion
15.9, 11, 12, 15, 20, 25, 31, 34, 35

| Return to Calendar |

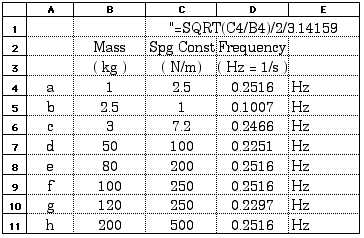
15.9 This is an excellent one to solve with a spreadsheet:


15.11 where k in this equation is the "effective spring constant", the spring constant of a single spring that has the same effect as the combination of springs in the diagram.


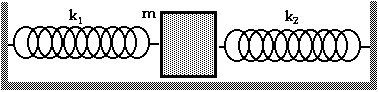
With this arrangement, a displacement of x causes a force of F1 = - k1x due to the spring on the left and a force of F2 = - k2x due to the spring on the right.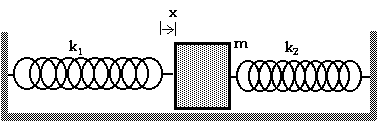

The net force, then, is Fnet = F1 + F2 = - k1x - k2x = - (k1 + k2)x. Since the effective spring constant, keff is the constant is Fnet = - keffx, we can see that

keff = k1 + k2

The next arrangement of springs is a little more "tricky" or more interesting:

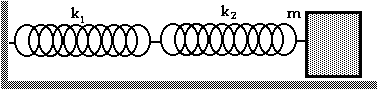
When the mass is moved a distance x, spring #1 stretches a distance x1 and spring #2 stretches a distance x2 with

x = x1 + x2

That is, the two springs need not be stretched (or compressed) the same amount at all. However, the force exerted by each spring must be the same. That is,

F1 = F2

or

k1 x1 = k2 x2

or

x1 = (k2/k1) x2

or

x2 = (k1/k2) x1

To determine the "effective spring constant", we must write the force in the form of

F = - keff x

We have

F = - k1 x1

and

x = x1 + x2
x = x1 + (k1/k2) x1
x = [ 1 + (k1/k2)] x1

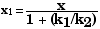
Therefore,

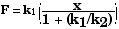
Therefore,

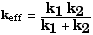
which can also be written as

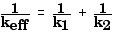
The third arrangement of springs is actually fairly easy and straightforward. With this arrangement, a displacement of x causes a force of F1 = - k1x due to spring #1 and a force of F2 = - k2x due to spring #2. The stretch of each spring is the same as the displacement of the mass.

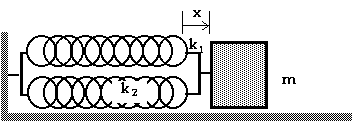
The net force, then, is Fnet = F1 + F2 = - k1x - k2x = - (k1 + k2)x. Since the effective spring constant, keff is the constant is Fnet = - keffx, we can see that

keff = k1 + k2

15.12

W = (1/2) k x2
W = (1/2) (80 N/m) (0.15 m)2
W = 0.9 J

15.15

W = PE = (1/2) k A2 = (1/2) (50 N/m) (0.1 m)2 = 0.25 J
As the mass moves through equilibrium, x = 0, so it has zero potential energy and its total energy is now KE,
KE = (1/2) m v2 = (1/2) (0.2 kg) v2 = 0.25 J = E
v2 = 2.5 m2/s2
v = 1.58 m/s

15.20 An object undergoes simple harmonic motion with an amplitude of 12 cm. At a point 8.0 cm from equilibrium, its speed is 20 cm/s. What is the period?

E = PEmax = (1/2) k A2

A = 12 cm = 0.12 m
E = (1/2) ( k ) (0.12 m)2
E = KE + PE = (1/2) m v2 + (1/2) k x2
E = (1/2) m (0.2 m/s)2 + (1/2) k (0.08 m)2 = (1/2) ( k ) (0.12 m)2 = E
m (0.2 m/s)2 = k (0.12 m)2 - k (0.08 m)2
(m/k)(0.2 m/s)2 = (0.12 m)2 - (0.08 m)2
(m/k)(0.04) (m/s)2 = (0.0144 - 0.0064) m2 = 0.0080 m2
(m/k) = 0.2 (1/s2)
T = 2 «
T = 2.8 sec

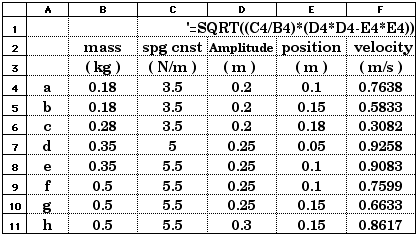
15.25 These multiple-data-set problems are good ones to solve with a spreadsheet. This is basically energy conservation,

E = (1/2) k A2 = (1/2) k x2 + (1/2) m v2
k A2 = k x2 + m v2
m v2 = k (A2 - x2)
v2 = (m/k) (A2 - x2)

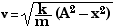
So this will be the formula we put in the spreadsheet:

15.31A 50-g (0.050 kg) mass hanging from a spring oscillates with a frequency of 2 Hz. What is the spring constant?

f 2 = (1/2 ) 2 (k/m)
f 2 = (1/4 2)(k/m)
k = 4 2 f 2 m
k = 4 2 [2 (1/s)] 2 (0.050 kg)
k = 3.95 kg/s2
k = 3.95 N/m

| Return to Calendar |

(c) 2000, Doug Davis; all rights reserved