

| Return to Calendar |
14.1 An ideal gas is sealed in a rigid container at 25°C and 1.0 atm. What will its temperature be when the pressure is incresed to 2.0 atm?
What will its pressure be when the temperature is increased to
50°C
The ideal gas law isPV = nRT Being in a rigid container, the gas’ volume does not change; V = Vo = constant. That means we can use the ideal gas law as
T/P = To/Po or
T = P [ To/Po ] = [ P/Po ] To Remember, these temperatures must be absolute temperatures,
To = 25°C = 302 K
T = [ P/Po ] To = [2.0 atm/1.0 atm] [302 K] = [ 2 ] [ 302 K] = 604 K
T = 604 K = (604 - 273)°C = 331°C = TOr, while V = const, we can write the ideal gas law as
P/T = Po/To or
P = T [ Po/To ] = [ T/To] Po Remember, these temperatures must be absolute temperatures, measured in Kelvins, K.
To = 25°C = 302 K and T = 50°C = 327 K
P = [ T/To ] Po
P = [ 327 K/302 K ] (1 atm)
P = 1.08 atm
14.17 Gas at 1.5 atm expands from 2.5 liters to 3.5 liters. How much work is done by the gas?
Work is the area under the curve on a p-V diagram; for constant pressure, this isW = p V
W = (1.5 atm)(1.0 l)
W = 1.5 atm-l = 1.5 l-atmWhile this is certainly true, a conversion to units of joules is called for,
1 l-atm = ( 10 - 3 m3 ) (1.013 x 10 5 N/m2) = 1.013 x 10 2 N-m = 101.3 J
W = 1.5 l-atm [ 101.3 J/1 l-atm ] = 152 J = W
W = 152 J
14.26 Under a constant pressure of 1.5 atm, a gas expands from 2.0 liters to 3.0 liters while 500 J of energy flows into it.
(a) How much work is done by the gas?
(b) What is the change in its internal energy?
Part (a) of this question is identical to question 14.17. We already know the answer to that; the work done by the gas isW = 152 J
As the gas does 152 J of work, it absorbs or receives 500 J of energy. That means its net increase in internal energy is
Eint = Q - W = 500 J - 152 J = 348 J
Eint = 348 J
(a) How much work is done on the gas?
(b) What is the change in its internal energy?Work is the area under the curve on a p-V diagram; for constant pressure, this is
W = p V
W = (2.25 atm) (- 0.50 l)
W = - 1.125 l-atm
W = - 1.125 l-atm [ 101.3 J/1 l-atm ] = - 114 JAs the gas does W = - 114 J of work (which is equivalent to having 114 J of work done on it), it also gives up 375 J of energy (which means Q = - 375 J). That means its net change in internal energy is
Eint = Q - W = - 375 J - (- 114 J)
Eint = - 261 J
14.37 After 1.0 mol of an ideal gas initially at 0°C and 1.0 atm expands isothermally to twice its initial volume, it is compressed isobarically back to its original volume. What is the net work done by or on the gas? What is its final temperature?
This calls for a p-V diagram.
When the gas expands isothermally from state 1 to state 2, the work done by the gas is given by Equation 14.17,
Wisotherm = n R T ln [Vf/Vi] or
Wisotherm = n R T ln [V2/V1] From the problem statement, we know
V2 = 2 V1 From this, we can calculate the work done by the gas,
Wisotherm = (1.0 mol)(8.314 J/mol-K) (273 K) ln[2 V1 /V1]
Wisotherm = (1.0 mol)(8.314 J/mol-K (273 K) ln[ 2 ]
Wisotherm = (1.0 mol)(8.314 J/mol-K ) (273 K) 0.693
Wisotherm = 1,573 JThis is the area under the curve from state 1 to state 2
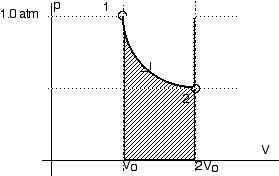
As the gas is compressed from state 2 to state 3 the work done is, as always, the area under the curve.
Wisobar = pV = p (Vo - 2 Vo) = - p Vo
We must find p, the pressure for state 2 or state 3. Since we got to state 2 by an isothermal expansion from state 1, we know the temperature at state 2 must be the same as at state 1; T1 = T2 = 273 K. We can then apply the ideal gas law or, more simply, just use
pV = constant ( for constant T )
p2 V2 = p1 V1
p2 = p1 (V1/V2) = (1.0 atm) (V1/2 V1) = 0.5 atm = p2
p2 = p1 (1/2) = 0.5 atmTo find the work done, Wisobar = - pVo, we need a numerical value for Vo, the initial volume. We could also call this V1, the volume at state 1. To find this initial volume Vo or V1, we use the ideal gas law,
pV = nRT Again, remember that temperatures are often given in degrees Celsius because that is “convenient” but temperatures in the ideal gas law must be absolute temperatures or temperatures on the Kelvin scale!
pV = nRT
(1.0 atm) (Vo) = (1.0 mol) (8.314 J/mol-K) (273 K)
(1.0 atm) [ (1.013 x 10 5 N/m2)/atm ] (Vo) = (1.0 mol) (8.314 J/mol-K ) (273 K)
[ 1.013 x 10 5 N/m2 ] (Vo) = (1.0 mol)(8.314 J/mol-K ) (273 K)
Vo = 2.24 x 10 - 2 m3
V1 = Vo = 2.24 x 10 - 2 m3Now we can go back to calculating the work done on/by the gas,
Wisobar = - p Vo = - (0.5 atm)(2.24 x 10 - 2 m3)
Wisobar = - p Vo = - (0.5 x 1.013 x 10 5 N/m2 )(2.24 x 10 - 2 m3)
Wisobar = - 1,135 J
Now we can add these two amounts of work together for the net work done.Wnet = W12 + W23
Wnet = Wisotherm + Wisobar
Wnet = 1,573 J + (-1,135 J)
Wnet = 438 J
This net work is the area shown on the graph above.
14.44 A heat engine absorbs 6 J from a source of heat and
does 2 J of mechanical work. What is its efficiency?
14.46 A reversible heat engine whose efficience is 15 percent does 180 J of work. How much heat does it absorb from the hot reservoir?
Qh = W / Eff
Qh = 180
J/0.15
Qh = 1,200 J
Remember, all these temperatures must be absolute temperatures. That means for our initial Carnot engine,Th = 650°C = (650 + 273) K = 923 K First, find Tc the temperature of the cold reservoir. That will remain the same.
Eff = 1 - Tc/Th = 0.30
Tc/Th = 1 - 0.30 = 0.70
Tc = 0.70 Th = (0.70) (923 K) = 646 K
( Tc = 373°C )Now, with this as the cold reservoir (Tc = 646 K), what temperature for the hot reservoir (Th = ?) will give an efficiency of 0.35?
Eff = 1 - Tc/Th = 0.35
Tc/Th = 1 - 0.35 = 0.65
Th = Tc/0.65Th = 646 K/0.65
Th = 993 K
( Th = 620°C )
14.58 The efficiency of a sasoline engine is 0.55. Estimate the
temperature of the combustion gases if the exhaust gases leave the
engine at 125°C.
To estimate the operation of a real engine, like a gasoline engine, we may treat it as if it were a reversible or Carnot engine. For such a Carnot engine, the efficiency isEff = 1 - Tc/Th The exhaust gases leave at the cold temperature of Tc = 125°C = 398 KTc/Th = 0.55
Tc/Th = 1.0 - 0.55 = 0.45
Th = 398 K/0.45
Th = 884 K
( Th = 611°C )
| Return to Calendar |
(c) 2000, Doug Davis; all rights reserved