PHYsics 1151

Homework

Chapter 13, Heat Transfer
Ch 13: 5, 17, 21, 24, 26, 30

| Return to Calendar |

13.5 A goose-down sleeping bag has a surface area of 2.25 m² and is filled with a layer of down 5 cm thick. What is the heat-transfer rate (H_cd) through it from a person with skin temperature of 35°C to the outside air at -5°C. How does this rate compare with the body’s minimal metabolism rate, about 100 W?

From Table 13,1, p 457, we find the thermal conductivity of goose down to be K = 0.023 W/m C°

We can now apply the conduction heat-transfer equation, Eq 13.1,

H_cd = [K A (T₂ - T₁)] / L

From the problem, we know the other pieces of this equation,

DT = T₂ - T₁ = 35°C - (- 5°C) = 40 C°
A = 2.25 m²
L = 5 cm = 0.05 m
H_cd = [K A (T₂ - T₁)] / L
H_cd = [(0.023 W/m C°)(2.25 m ²)(40 C°)]/0.05 m =
H_cd = 41 W

This is about half of the body’s normal metabolism so this sleeping bag should keep our camper a “happy camper” (or, at least, a warm camper).

(Hmmm, . . . go ahead and use e = 1.00, even in this case).

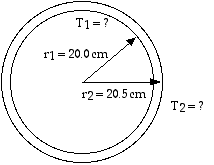
To find the temperature, we can use the Radiation equation, Eq 13.4, R_emit = e A T ⁴

We will use e 1.0, even for this. s is the Stefan-Boltzman constant,

= 5.67 x 10 ^{- 8} W/_m2 _K4

The surface area of a sphere is

A = (4) r ²

Earlier, I was wrong. The volume of a sphere is (⁴/₃) r ³ and I had confused pieces of that equation with this one, that the surface area of a sphere is

A = (4) r ²

For the inner surface,

A_inner = (4) (0.200 m)² = 0.50265 m²

For the outer surface,

A_out = (4) (0.205 m)² = 0.5281 m²

The temperatures T must be absolute temperatures, measured on the Kelvin scale.
Now we are ready to solve for the temperaturs

T ⁴ = R_emit / e A
T_inner⁴ = 100 W/[(1.0)(5.67 x 10 ^{- 8} W/m² K⁴)(0.50265 m²)] = 3.509 x 10 ⁹ K⁴
T_inner = 243 K
T_outer⁴ = 100 W/[(1.0)(5.67 x 10 ^{- 8} W/m² K⁴)(0.5281 m²)] = 3.3396 x 10 ⁹ K⁴
T_outer = 240 K

Our use of e = 1.0 , for the emissivity, makes our actual numbers rather “iffy”. But the point of this problem was to show that the inner surface will be at a higher temperature than the outer surface. That is certainly true for our calculation. Changing the value of the emissivity e may change our actual numbers but we will still find T_inner > T_outer.

13. 21 Victoria, [BC,] Canada, is located at 48.5° north latitude. How high above the horizon is the Sun on the first day of summer and the first day of winter?

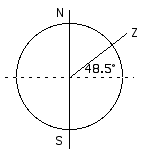
N and S mark the poles, the axis of rotation. Z is the zenith, the point directly overhead, 48.5° from the equator (48.5° north latitude).

Summer:

is the angle from directly overhead (the zenith) to the Sun. Therefore, the angle between the horizon and the Sun will be 90° - = 90° - 25° = 65°. The Sun will be 65° above the horizon at the summer solstice.

Winter:

is again the angle between directly overhead (the zenith) and the Sun. Therefore, the Sun is 90° - 72° = 18° above the horizon at the winter solstice.

13.24 A solar home is to be built in Minneapolis, 45° north latitude. What is the elevation of the Sun at midday on the first day of summer and on the first day of winter? An overhaning eave 85 cm wide is planned. How far below this eave will sunlight fall on the first day of summer and the first day of winter.

The first part of this questions requires exactly the same reasoning, using exactly the same kind of diagrams, as question 13.21.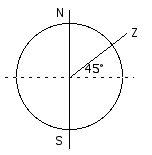

N and S mark the poles, the axis of rot ation. Z is the zenith, the point directly overhead, 45° from the equator (45° north latitude).

Summer: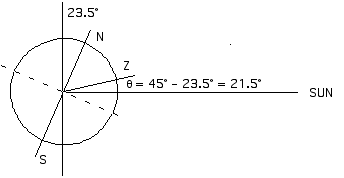

If the Sun is 21.5° from the zenith (the position directly overhead) then it must be 90° - 21.5° = 68.5° above the horizon.

Winter: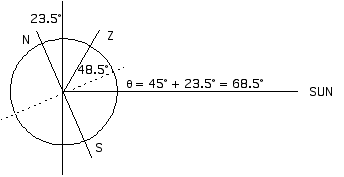

If the Sun is 68.5° from the zenith, then it must be 90° - 68.5° = 21.5° above the horizon.
Now we can look at the shadow cast by the eave on these two days:

Summer: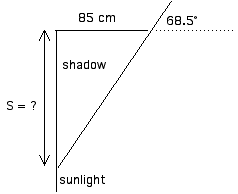

The length of the shadow, S in the diagram, is the opposite side of a 68.5° right triangle (85 cm is the adjacent side).

tan = ^opp/_adj
tan 68.5° = ^S / _{85 cm}
S = (85 cm)(tan 68.5°)
S = (85 cm)(2.54) = 216 cm = 2.16 cm

Winter:

The length of the shadow, S in the diagram, is the opposite side of a 21.5° right triangle (85 cm is the adjacent side).

tan = ^opp/_adj
tan 21.5° = ^S / _{85 cm}
S = (85 cm)(tan 21.5°)
S = (85 cm)(0.393) = 33.5 cm

---

13.26 Calculate the R value of an insulated wall like that in Figure 13.30 if 2 x 6’s are used for wall studs instead of 2 x 4’s. The larger board allow 5.5 in of fiberglass insulation instead of 3.5 in.

By what percentage does this increase in thickness change the R value?
How does the increased thickness change the heat loss calculated in Example 13.14?
The R-values for the components of the wall in Figure 13.30 are given in Table 13.4, on page 481. By increasing the fiberglass insulation from 3.5 inches to 5.5 inches, the R-value for this insulation increases from 10.90 to 18.80, according to Table 13.3, on page 480. This increases the total R-value from 14.33 to 22.23.
This is an increase of ^7.9/_14.33 = 0.55 = 55% for the R-value of the wall.
In terms of R-values, the conduction heat transfer rate is given by equation 13.9, H_cd = A (T₂ - T₁) / R = (¹/_R) [A (T₂ - T₁)]

In Example 13.14, we found the conduction heat transfer rate to be

H_cd(un) = 3.8 kW

for the uninsulated wall,

H_cd(3.5) = 1.2 kW

for the insulated wall with 2x4’s and 3.5 in of insulation
Now, with 2x6’s and 5.5 in of insulation,

H_cd(5.5) = (¹/_22.23)[(960)(60)] = 2591 Btu/h = 0.76 kW

This is a reduction of heat flow by

H = 1.18 kW - 0.76 kW = 0.42 kW
H / H = ^{0.42 kW} / _{1.18 kW} = 0.36 = 36%

This requires an application of Newton’s Law of Cooling, equation 13.3, T(t) = T_sur + T e^{- t/}

T is the initial temperature difference of the turkey and its surroundings;

T = 85°C - 25°C = 60 C°

Knowing that it cools from 85°C to 80°C allows us to solve for the “time constant” t in this equation;

T(t) = T_sur + T e^-t/
T(10 min) = 80°C = 25°C + (60 C°) e^{-( 10 min)/}
55°C = (60 C°) e^{- (10 min)/
55°C}/_60°C = e^{- (10 min)/
55}/₆₀ = e^{- (10 min)/t}
0.9167 = e^{- (10 min)/}
e^{- (10 min)/} = 0.9167
ln[e^{- (10 min)/} ] = ln[0.9167]
- (10 min)/ = -0.0870
10 min/ = 0.0870
= (10 min)/0.0870
= 115 min

Now we know the time constant t and we can use Newton’s Law of Cooling to go back and solve for t, the time, when T, the temperature, is 55°C.

T(t) = T_sur + T e^{- t/}
T(t) = 55°C = 25°C + (60 C°) e^{-t /(115 min)}
55°C = 25°C + (60 C°) e^{- t/(115 min)}
30°C = (60 C°) e^{- t/(115 min)
30°C}/_60°C = e^{- t/(115 min)
30}/₆₀ = e^{- t /(115 min)}
0.50 = e^{- t/(115 min)}
ln[0.50] = ln[e^{- t/(115 min)}]
-0.693 = -t/(115 min)
0.693 = t/(115 min)
t = (0.693)(115 min)
t = 78 min

| Return to Calendar |

 

(c) 2000, Doug Davis; all rights reserved