PHYsics 1151

Homework

Chapter 12; Temperature, Heat, and Internal Energy
Ch 12: 2, 10, 29, 32, 40, 41, 47, 50, 57, 59, 61

| Return to Calendar |

 

12.2 If you have a fever of 102° on a Fahrenheit thermometer, what is your temperature on a Celsius thermometer?

TC = [5/9] [TF - 32°F ]
TC = [5/9] [102°F - 32°F ]
TC = [5/9] [70 F° ]
TC = [5 C°/9 F°] [70 F° ]
TC = 39°C

12.10 On a concrete road, how large should the expansion joints be between sections if each section is 15 m long. Consider a temperature range of -10°C to + 35°C.

l = lo T

From Table 12.1, p 430, we find the coefficient of thermal expansion for concrete to be

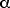= 12 x 10-6 (C°)-1
l = [12 x 10-6 (C°)-1] [15 m] [45 C°]
l =8.1 x 10-3 m
l = 8.1 mm

12.29 A steel surveying tape is carefully calibrated at 20°C. However, it is used on a 38°C summer day. Are the distances measured too large or too small? What is the percentage of error introduced by this temperature change?


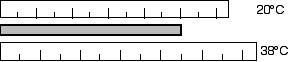
Due to the increase in temperature, the tape will elongate or get longer. The length measured with the longer surveying tape will be too small.

l = lo T

From Table 12.1, p 430, we find the coefficient of thermal expansion for steel to be

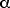= 12 x 10-6 (C°)-1
l = [12 x 10-6 (C°)-1] [ lo] [18 C°]
l =2.16 x 10-4 lo = 2.2 x 10-4 lo
l/lo = .0022 = 0.22%

(not a very big change, of course!)

12.32 If concrete roadway sections are poured butted against each other when the temperature is 15°C, what will the thermal stress be when the temperature reaches 40°C? Young’s modulus for concrete is about 20 x 109 Pa.

The thermal stress is given by Equation 12.3

F/A = 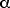Y T

From Table 12.1, p 430, we have the coefficient of linear expansion for concrete,

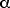= 12 x 10-6 (C°)-1
F/A = 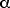Y T
F/A = [12 x 10-6 (C°)-1] [20 x 109 Pa] [25 C°]
F/A = 6 x 106 Pa

12.40 A home furnace is rated at 50,000 Btu/h. What is this power rating in kilowatts?

The conversion from Btu to J is given on p 437.

P = 50,000 Btu/h = 50,000 Btu/h [1054.8 J/Btu][h/3600 s] = 1.465 x 104 J/s
P = 1.465 x 104 J/s = 14.65 x 103 J/s [W/(J/s)] = 14.65 x 103 W = 14.67 kW

12.41. A child’s wading pool contains 1.2 m3 of water at 15°C. How much heat must be added to the pool to bring the temperature to 27°C?

Equation 12.5 gives us the heat needed -- but in terms of the mass of the water. What is the mass of 1.2 m3 of water?

m = 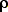V = (1000 kg/m3)(1.2 m3) = 1.2 x 103 kg = 1,200 kg
Q = c m T
Q = [4186 J/kg C°] [1,200 kg] [12 C°]
Q =6.03 x 107 J

12.47 Once its melting point is reached, how much heat is required to melt a 0.5 kg bar of gold?

From Table 12.3, p 440, the Heat of Fusion for gold is Lf = 0.644 x 105 J/kg

Q = Lf m
Q = [ 0.644 x 105 J/kg ] [ 0.5 kg ] = 0.322 x 105 J = 3.22 x 104 J = 32,200 J

12.50 If 0.60 kg of boiling hot coffee is poured into a 0.250-kg steel camping cup initially at 20°C, what is the final temperature of the cup-coffee system?

Q1 + Q2 = 0
Q1 = Qcup = ccup mcup Tcup = csteel msteel Tsteel

From Table 12.2, p 438, we find that the specific heat of steel is csteel = 450 J/kg C°

Q1 = csteel msteel Tsteel = ( 450 J/kg C° ) (0.250 kg) (Tf - 20°C)
Q2 = Qcoffee = ccoffee mcoffee Tcoffee = cwater mwater Twater
Q2 = cwater mwater Twater = (4186 J/kg C°) (0.60 kg) (Tf - 100°C)

where we have taken the specific heat of coffee to be the same as the specific heat of water,

ccoffee = cwater = 4186 J/kg C°.

Now we can put these all together as

Q1 + Q2 = 0
( 450 J/kg C° ) (0.250 kg) (Tf - 20°C) + (4186 J/kg C°) (0.60 kg) (Tf - 100°C) = 0
112.5 (J/C°) Tf - 2,250 J + 2,512(J/C°) Tf - 251,200 J = 0
112.5 (J/C°) Tf + 2,512(J/C°) Tf = 2,250 J + 251,200 J
[ 112.5 + 2,512 ](J/C°) Tf = [ 2,250 + 251,200 ] J
2,624.5 Tf = 253,450 °C
Tf = 253,450 °C/2,624.5
Tf = 96.6°C

12.57 A 0.050-kg ice cube, initially at - 5.0°C, is placed in 0.30 kg of water at 25°C. What is the final temperature of the water? Or, if melting is not complete, how much ice remains unmelted at thermal equilibrium? Assume no heat is lost to the environment.

First, assume all the ice melts, so Tf > 0°C

Q1 + Q2 = 0
Q1 = heat lost by the water
Q1 = cwater mwater Twater = (4186 J/kg C°)(0.30 kg)(Tf - 25°C)
Q1 = (4186 J/kg C°)(0.30 kg)(Tf - 25°C) = 1,256 (J/C°) Tf - 31,395 J

Q2 = heat gained by ice
Q2 = heat gained in raising ice to 0°C +
+ heat gained in melting ice +
+ heat gained in raising the melted ice (now water) to temperature Tf
Q2 = cice mice T1 + Lf,ice mice + cwater mice T2
Q2 = [2090 J/kg C°][0.05 kg][0°C - (- 5°C)] +
+ [3.33 x 105 J/kg][0.05 kg] +
+ [4186 J/kg C°][0.05 kg][Tf - 0°C]

Be very careful with these temperature changes!

Q2 = 522.5 J + 16,650 J + 209.3 (J/C°) Tf - 0
Q2 = 17,172.5 J + 209.3 (J/C°) Tf

Now we are ready to go back to

Q1 + Q2 = 0
1,256 (J/C°) Tf - 31,395 J + 17,172.5 J + 209.3 (J/C°) Tf = 0
1,256 (J/C°) Tf + 209.3 (J/C°) Tf = 31,395 J - 17,172.5 J
1,465 (J/C°) Tf = 14,222 J
Tf = [14,222/1,465]°C
Tf = 9.7°C

And this is a reasonable answer.

12.59 A 0.15-kg ice cube initially at -15°C is placed in 0.30 kg of water at 25°C. What is the final temperature of the water? Or, if melting is not complete, how much ice remains unmelted at thermal equilibrium? Assume no heat is lost to the environment.

This should look very similar to problem 12.57. Now we have a larger and colder ice cube.

First, assume all the ice melts, so Tf > 0°C

Q1 + Q2 = 0
Q1 = heat lost by the water
Q1 = cwater mwater Twater = (4186 J/kg C°)(0.30 kg)(Tf - 25°C)
Q1 = (4186 J/kg C°)(0.30 kg)(Tf - 25°C) = 1,256 (J/C°) Tf - 31,395 J

Q2 = heat gained by ice
Q2 = heat gained in raising ice to 0°C +
+ heat gained in melting ice +
+ heat gained in raising the melted ice (now water) to temperature Tf
Q2 = cice mice T1 + Lf,ice mice + cwater mice T2
Q2 = [2090 J/kg C°][0.15 kg][0°C - (- 15°C)] +
+ [3.33 x 105 J/kg][0.15 kg] +
+ [4186 J/kg C°][0.15 kg][Tf - 0°C]

Be very careful with these temperature changes!

Q2 = 4,702 J + 49,950 J + 628(J/C°)Tf - 0
Q2 = 54,652 J + 628(J/C°)Tf

Q1 + Q2 = 0
1,256 (J/C°) Tf - 31,395 J + 54,652 J + 628 (J/C°)Tf = 0
[1,256 + 628](J/C°)Tf + [- 31,395 + 54,652]J = 0
1,884](J/C°)Tf + 23,257J = 0
1,884](J/C°)Tf = - 23,257J
Tf = [- 23,257/1,884]°C
Tf = - 12.3°C

And this is inconsistent with our assumption that Tf > 0. Therefore, we have to look at another possibility. This time, we shall assume Tf = 0°C and only mmelt of the ice melts. Our calculation for Q1 is almost the same as before but our calculation for Q2 is quite different.

Q1 = heat lost by the water
Q1 = cwater mwater Twater = (4186 J/kg C°)(0.30 kg)(0°C - 25°C)
Q1 = (4186 J/kg C°)(0.30 kg)(- 25°C) = - 31,395 J

Q2 = heat gained by ice
Q2 = heat gained in raising ice to 0°C + heat gained in melting some ice
Q2 = cice mice T1 + Lf,ice mmelt
Q2 = [2090 J/kg C°][0.15 kg][0°C - (- 15°C)] + [3.33 x 105 J/kg][mmelt]
Q2 = 4,702 J + 3.33 x 105 (J/kg)mmelt
Q1 + Q2 = 0
- 31,395 J + 4,702 J + 3.33 x 105 (J/kg)mmelt = 0
- 26,693 J + 3.33 x 105 (J/kg)mmelt = 0
3.33 x 105 (J/kg)mmelt = 26,693 J
mmelt = [26,693/333,000] kg
mmelt = 0.080 kg

Since we started with 0.150 kg, this is a reasonable answer. There will remain 0.070 kg of ice that has not melted.

12.61 The inside diameter of a steel lid and the outside diameter of a glass peanut butter jar are both exactly 11.50 cm at room temperature, 21.0°C. If the lid is stuck and you run 80°C hot water over it until the lid and the jar top both come to 80°C, what will the new diameters be?

For the steel lid, the change in the diameter, d, is

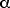d = do T = [12 x 10- 6(C°)-1] [11.50 cm] [59 C°] = 0.0081 cm

so the new diameter is

dnew = do + d = 11.5081 cm

For the glass jar, the change in the diameter, Dd, is

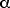d = do T = [10 x 10- 6(C°)-1] [11.50 cm] [59 C°] = 0.0068 cm

so the new diameter is

dnew = do + d = 11.5068 cm

Now the difference in the two diameters is 0.0013 cm. That may be enough to break the lid loose and let us make our peanut butter sandwich!

| Return to Calendar |

 

(c)2000, Doug Davis; all rights reserved